Числовые множества

Содержание

Предисловие…………………………………………………………………..
1.	Числовые множества…………………………………………………..
	1.1.	Натуральные и целые числа……………………………………...
	1.2.	Рациональные числа………………………………………….......
	1.3.	Иррациональные числа…………………………………………...
	1.4.	Действительные числа. Числовые промежутки………………...
	1.5.	Модуль действительного числа………………………………….
	1.6.	Метод математической индукции……………………………….
	Задачи для самостоятельного решения………………………………...
2.	Функции действительного переменного…………………………….
	2.1.	Понятие функции……………………………………………........
	2.2.	Свойства функции………………………………………………..
	2.3.	Основные элементарные функции…………………………........
	2.4.	Элементарные функции. Классификация функций…………….
	2.5.	Геометрические преобразования графиков……………………..
	Задачи для самостоятельного решения………………………………...
3.	Степени. Многочлены. Корни. Алгебраические выражения…….
	3.1.	Степень действительного числа…………………………….........
	3.2.	Многочлены. Действия над многочленами……………………..
	3.3.	Преобразование алгебраических выражений…………………...
	Задачи для самостоятельного решения………………………………...
4.	Уравнения……………………………………………………………….
	4.1.	Основные понятия………………………………………………...
	4.2.	Линейные уравнения……………………………………………...
	4.3.	Квадратные уравнения и уравнения, сводящиеся к ним……….
	4.4.	Рациональные и дробно-рациональные уравнения……………..
	4.5.	Уравнения с модулем……………………………………………..
	4.6.	Иррациональные уравнения………………………………….......
	Задачи для самостоятельного решения………………………………...

5.	Неравенства……………………………………………………………….
	5.1.	Основные понятия………………………………………………....
	5.2.	Квадратные неравенства…………………………………………..
	5.3.	Рациональные и дробно-рациональные неравенства. Метод интервалов для рациональных неравенств…………………….....
	5.4.	Неравенства с модулем………………………………………….....
	5.5.	Иррациональные неравенства……………………………………..
	Задачи для самостоятельного решения………………………………......
6.	Показательные уравнения и неравенства…………………………….
	6.1.	Показательные уравнения…………………………………………
	6.2.	Показательные неравенства…………………………………….....
	Задачи для самостоятельного решения………………………………......
7.	Логарифмические уравнения…………………………………………..
	7.1.	Преобразование логарифмических выражений..………………...
	7.2.	Логарифмические уравнения……………………………………...
	7.3.	Логарифмические неравенства……………………………………
	Задачи для самостоятельного решения………………………………......
8.	Тригонометрия……………………………………………………………
	8.1.	Преобразование тригонометрических выражений………………
	8.2.	Тригонометрические уравнения…………………………………..
	8.3.	Тригонометрические неравенства………………………………...
	Задачи для самостоятельного решения……………………………….....
9.	Системы уравнений……………………………………………………..
	9.1.	Основные понятия………………………………………………....
	9.2.	Методы решения систем алгебраических уравнений…………...
	9.3.	Системы иррациональных уравнений…………………………....
	9.4.	Системы показательных и логарифмических уравнений……….
	9.5.	Системы тригонометрических уравнений……………………….
	Задачи для самостоятельного решения……………………………….....
10.	Дифференциальное исчисление функции одной переменной……..
	10.1.	Понятие производной функции. Правила дифференцирования...
	10.2.	Приложения производной…………………………………………
	Задачи для самостоятельного решения…………………………………..
11.	Комплексные числа……………………………………………………...
	11.1.	Определение комплексного числа………………………………..
	11.2.	Действия над комплексными числами……………………………
	11.3.	Тригонометрическая и показательная формы комплексного числа………………………………………………………………...
	11.4.	Множества комплексной плоскости……………………………....
	Задачи для самостоятельного решения…………………………………..
Литература……………………………………………………………………...
Краткий теоретический справочник………………………………………..

Предисловие

структура

содержание

кому полезно

незамкнутое

задачи для самостоятельного решения по блокам с ответами

краткий теоретический справочник

Числовые множества

Понятие множество используется в математике для описания совокупности предметов или объектов. При этом предполагается, что предметы (объекты) этой совокупности можно отличить друг от друга и от предметов, не входящих в данную совокупность. Например, можно говорить о множестве всех учеников данного класса, множестве всех вершин данного многогранника, множестве всех целых чисел, множестве всех точек отрезка. При этом ученики данного класса, вершины данного многогранника, целые числа, точки данного отрезка являются элементами соответствующих множеств.

Обычно множества обозначаются большими буквами А тот факт, что объект является элементом множества 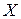, записывается так: и читается « принадлежит множеству 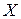». Запись означает, что не является элементом множества .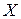

Если множество 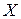представляет собой часть множества 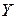, то говорят, что множество 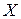является подмножеством множества 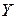и обозначают 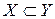. Знак «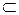» называют знаком включения.

Дата добавления: 2015-07-10