Натуральные и целые числа

Числа, которые используют при счете предметов, то есть 1, 2, 3, 4, 5, …, называют натуральными числами. Для записи натуральных чисел пользуются цифрами 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Натуральные числа можно складывать и перемножать. При этом результате получится натуральное число. Результат же операций деления и разности натуральных чисел не всегда является натуральным числом: например, разность 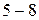не является натуральным числом.

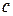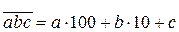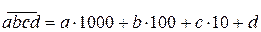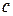Число, которое состоит из сотен, десятков и единиц, записывают в виде . Аналогично, , где - цифра тысяч, - цифра сотен, - цифра десятков, 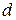- цифра единиц.

Более широкий класс чисел составляют целые числа. К ним относят натуральные числа, число 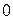и числа -1, -2, -3, -4, …. Над целыми числами выполнимы операции сложения, умножения и вычитания.

Множество натуральных чисел обозначают буквой 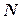, множество целых чисел – буквой 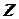. Очевидно, что множество натуральных чисел является подмножеством множества целых чисел, то есть .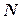

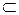
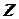Рассмотрим далее вопрос делимости натуральных чисел.

Определение 1.1. Пусть даны два натуральных числа - и . Если существует натуральное число 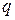такое, что выполняется равенство 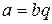, то говорят, что число делится на число . При этом число называют делимым, - делителем, 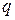- частным. Число называют также кратным числа .

Если число делится на число , то используют обозначение: .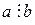

Опираясь на определение 1.1, можно получить ряд свойств отношения делимости на множестве натуральных числах.

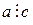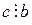Свойство 1. Если и , то .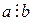

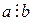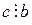Свойство 2. Если и , то .

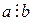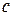Свойство 3. Если и не делится на , то 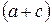не делится на .

Свойство 4. Если 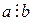и , то .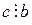

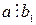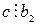Свойство 5. Если и , то .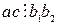

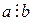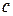Свойство 6. Если и - любое натуральное число, то 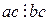; если 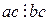, то .

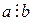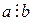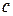Свойство 7. Если и - любое натуральное число, то .

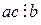Свойство 8. Есл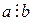и и 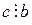, то для любых натуральных чисел и 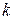справедливо соотношение .

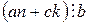Свойство 9. Среди последовательных натуральных чисел одно и только одно делится на .

Пример 1.1. Доказать, что для любого натурального числа 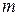число 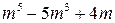делится на 2, 3, 4, 5, 8.

Решение. Разложим многочлен 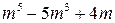на множители:

.

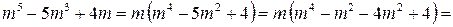
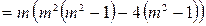
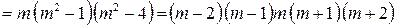Рассмотрим полученное произведение. При 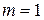, 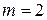оно обращается в 0, значит, делится на 2, 3, 4, 5, 8. При 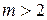имеем произведение пяти последовательных натуральных чисел 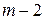, , 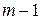, , 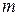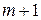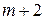. Из этих пяти чисел, по свойству 9, одно обязательно делится на 5, хотя бы одно – на 3, хотя бы одно – на 4, и кроме того есть еще хотя бы одно четное число, то есть число, делящееся на 2. Тогда, по свойствам, 5 и 7, произведение этих пяти чисел делится на 2, 3, 4, 5 и на произведение чисел 2 и 4, то есть делится на 8.

Рассмотрим далее признаки делимости - на 2, 3, 4, 5 и т. д.

Признак делимости на 2. Для того чтобы натуральное число делилось на 2, необходимо и достаточно, чтобы последняя цифра числа делилась на 2.

Признак делимости на 5. Для того чтобы натуральное число делилось на 5, необходимо и достаточно, чтобы последняя цифра числа делилась на 5 (то есть цифра единиц 0, либо 5.)

Признак делимости на 10. Для того чтобы натуральное число делилось на 10, необходимо и достаточно, чтобы цифра единиц была 0.

Признак делимости на 4. Для того чтобы натуральное число , содержащее не менее трех цифр, делилось на 4, необходимо и достаточно, чтобы делилось на 4 число, образованное двумя последними цифрами числа .

Признак делимости на 25. Для того чтобы натуральное число , содержащее не менее трех цифр, делилось на 25, необходимо и достаточно, чтобы делилось на 25 число, образованное двумя последними цифрами данного числа .

Признак делимости на 8. Для того чтобы натуральное число , содержащее не менее четырех цифр, делилось на 8, необходимо и достаточно, чтобы делилось на 8 число, образованное тремя последними цифрами числа .

Признак делимости на 125. Для того чтобы натуральное число , содержащее не менее четырех цифр, делилось на 125, необходимо и достаточно, чтобы делилось на 125 число, образованное тремя последними цифрами числа .

Признак делимости на 3. Для того чтобы натуральное число , делилось на 3, необходимо и достаточно, чтобы сумма его цифр делилась на 3.

Признак делимости на 9. Для того чтобы натуральное число , делилось на 9, необходимо и достаточно, чтобы сумма его цифр делилась на 9.

Пример 1.2. Найти пятизначное число, кратное 45, если известно, что каждая из трех его средних цифр на 1 больше предыдущей.

Решение. Пусть 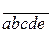- искомое число. Так как по условию каждая из цифр , , 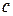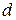на 1 больше предыдущей, то 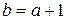, , 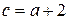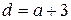. Искомое число делится на 45, следовательно, по свойству 1 оно делится на 5 и на 9. Поскольку число делится на 5, последняя цифра может принимать только два значения: 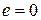или 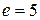. Рассмотрим отдельно оба этих случая.

1) Пусть 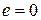. Тогда сумма цифр искомого числа равна

.

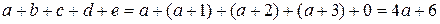По условию искомое число делится на 9. Согласно признаку делимости на 9 это означает, что сумма цифр искомого числа делится на 9, то есть 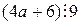. Найдем такие значения , при которых это условие выполнено. Так как 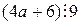, то по свойству 1, 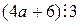, или, что то же самое, 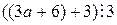. Но 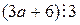, тогда по свойству 4 - 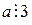. Следовательно, для первой цифры искомого числа есть следующие возможности: 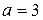, , 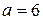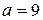. Цифру 9 можно сразу исключить, так как в этом случае 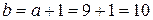- не цифра.

Если 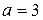, то 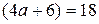, а 18 делится на 9. Значение 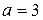нам подходит.

Если 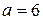, то 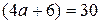, 30 не делится на 9, значит 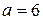нам не подходит.

Итак, при 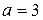получаем 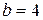, , 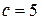, 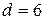а искомое число - 34 560.

2) Пусть 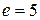. Тогда сумма цифр искомого числа равна

.

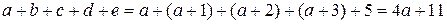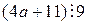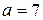По условию искомое число делится на 9. Следовательно, . Полагая последовательно равным 1, 2, 3, 4, 5, 6 ( не подходит, так как в этом случае 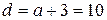- не цифра; тем более не подходят 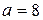, 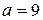), убеждаемся, что соотношение 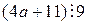выполняется лишь при ().

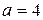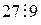Если 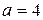, то 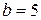, , 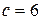, 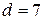а само искомое число – 45 675.

Ответ: 34 560; 45 675.

Признак делимости на 11. Для того чтобы натуральное число, делилось на 11, необходимо и достаточно, чтобы алгебраическая сумма его цифр, взятых со знаком «плюс», если цифры находятся на нечетных местах (начиная с цифры единиц), и взятых со знаком «минус», если цифры находятся на четных местах, делилась на 11.

Например, для числа 64 482 алгебраическая сумма, о которой идет речь формулировке признака, имеет вид 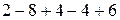и равна 0. Так как число 0 делится на 11, то и число 64 482 делится на 11.

Признак делимости на 7 (на 13). Для того чтобы натуральное число, делилось на 7 (на 13), необходимо и достаточно, чтобы алгебраическая сумма чисел, образующих грани по три цифры (начиная с цифры единиц), взятых со знаком «плюс» для нечетных граней и со знаком «минус» для четных граней, делилась на 7 (на 13).

Покажем, например, что число 254 390 815 делится на 7 и не делится на 13. Для этого разобьем число на грани 254, 390, 815. Составим алгебраическую сумму граней, начиная с последней грани и чередуя знаки «плюс» и «минус»: 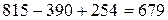. Число 679 делится на 7 и не делится на 13, значит, и заданное число делится на 7 и не делится на 13.

Определение 1.2. Если натуральное число имеет только два делителя – само себя и 1, то его называют простым числом; если оно имеет более двух делителей, то его называют составным числом.

Число 1, имеющее лишь один делитель – 1, не относят ни к простым, ни к составным.

Теорема 1.1. Любое натуральное число 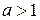имеет хотя бы один простой делитель.

Если натуральное число не делится на натуральное число , то рассматривают деление с остатком. Например, при делении числа 39 на число 14 в частном получается 2 (неполное частное) и в остатке 11. При этом имеет место соотношение 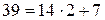. В общем случае справедлива следующая теорема.

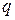Теорема 1.2. Если натуральное число больше натурального числа и не делится на , то существует, и только одна, пара натуральных чисел и 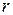, причем 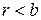, такая, что выполняется равенство

.

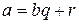(1.1)

Пример 1.3. Доказать, что если натуральное число 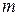при делении на 3 дает в остатке 2, то оно не может быть точным квадратом.

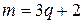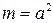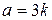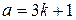Решение. По условию . Предположим, что это число является точным квадратом, то есть существует такое натуральное число , что . Для самого числа есть три возможности: делится на 3, то есть имеет вид ; при делении на 3 дает в остатке 1, то есть имеет вид ; при делении на 3 дает в остатке 2, то есть имеет вид .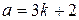

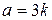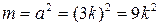1) Если , то . Это число делится на 3, что противоречит условию.

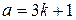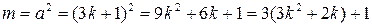2) Если , то . Это число дает при делении на 3 дает в остатке 1, что противоречит условию.

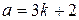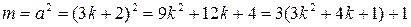3) Если , то . Это число дает при делении на 3 дает в остатке 1, что опять противоречит условию.

Таким образом, во всех возможных случаях приходим к противоречию. Следовательно, сделанное предположение неверно, то есть заданное число 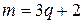не является точным квадратом.

Определение 1.3. Общим делителем натуральных чисел называется натуральное число, служащее делителем для каждого из них.

Определение 1.4. Наибольшим общим делителем (НОД) натуральных чисел называется наибольшее натуральное число, являющееся делителем всех данных чисел.

Дата добавления: 2015-07-10