|
Читайте также: |
Определение 2.9. Числовые промежутки, на которых функция сохраняет свой знак (то есть остается положительной или отрицательной), называются промежутками знакопостоянства.
| 
| О промежутках знакопостоянства легко судить по ее графику. Рассмотрим, например, функцию  (рисунок 2.6).
Здесь
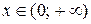 при  ,  при  .
|
| рис. 2.6 | рис. 2.7 |
В первом случае график расположен выше оси абсцисс, во втором – ниже.
Определение 2.10. Значения аргумента 
, при которых 
, называются корнями (или нулями) функции.
Значения аргумента, при которых функция обращается в ноль, - это абсциссы точек пересечения графика с осью Ох (рисунок 2.7).
Пример 2.8. Найти нули функции:
.
Решение. Решим уравнение
,
, 
, 
.
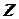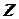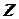Ответ: 
, .
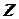Дата добавления: 2015-07-10; просмотров: 127 | Нарушение авторских прав