Периодические функции

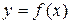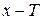Определение 2.8. Функция называется периодической, если существует такое число , что при любом из области определения функции числа и также принадлежат этой области определения и выполняется равенство

.

В этом случае число называется периодом функции .

Замечание 2.2. Если - период функции, то , где 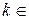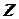, , также период функции. Следовательно, всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривают наименьший положительный период.

Замечание 2.3. Значения периодической функции повторяются через промежуток, равный периоду. Это обстоятельство используется при построении графиков.

Пример 2.7. Найти период функций:

а) ; б) ;

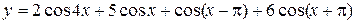в) ; г) ;

Решение. а) , .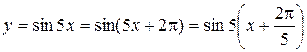

б) , .

в)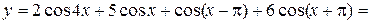

; .

г) . Рассмотрим первое слагаемое данной функции: 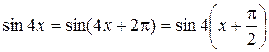, следовательно, . Для второго слагаемого имеем 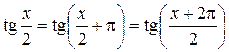, откуда .

Периодом исходной функции будет наименьшее кратное периодов ее слагаемых, то есть .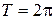

Ответ: а) ; б) ; в) ; г) .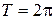

Дата добавления: 2015-07-10