Обратная функция

Пусть 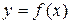есть функция от независимой переменной , определенной на промежутке 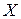с областью значений 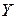. Поставим в соответствие каждому единственное значение , при котором 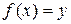. Тогда полученная функция , определенная на промежутке 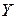с областью значений 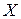, называется обратной.

Так как обычно независимую переменную обозначают через , а функцию через , то функция, обратная к функции 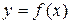, примет вид . Обратную функцию так же обозначают . Например, для функции обратной будет функция или .

Обратная функция существует для любой строго монотонной функции.

Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов.

Пример 2.9. Для данных функций записать обратную:

а) ; б) ; в) .

Решение. а) Функция возрастает на всей числовой оси, следовательно, для любых справедливо , то есть функция взаимно-однозначная, а значит, на всей числовой оси она имеет обратную функцию. Разрешим уравнение относительно . Имеем: или в привычном виде 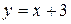( - функция, - аргумент).

б) Функция убывает на всей области определения: 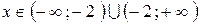. Следовательно, она имеет обратную функцию, которую можно найти, решив относительно уравнение . Получаем:

,

или в привычном виде: .

в) Функция возрастает на промежутке и, следовательно, имеет на нем обратную функцию. Найдем ее, решив на ОДЗ относительно уравнение :

,

или, окончательно получаем: .

Ответ: а) 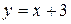; б) ; в) .

Дата добавления: 2015-07-10