
Читайте также:
|
Определение 3.1. Степенью действительного числа  с натуральным показателем
с натуральным показателем  (
(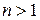 ) называют произведение
) называют произведение  множителей, каждый из которых равен
множителей, каждый из которых равен  . Степень числа
. Степень числа  с показателем
с показателем  обозначают
обозначают  . Таким образом,
. Таким образом,
 .
.
По определению считают:  , если
, если  ; выражение
; выражение  не определено. Кроме того, справедливы следующие свойства степени с натуральным показателем:
не определено. Кроме того, справедливы следующие свойства степени с натуральным показателем:
1. 
| 4. 
|
2. 
| 5. 
|
3. 
| 6. 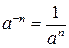 , , 
|
Замечание 3.1. Приведенные правила действия верны и для степеней с действительными показателями.
Определение 3.2. Корнем  -й степени из действительного числа
-й степени из действительного числа  называют действительное число
называют действительное число  ,
,  -ястепень которого равна
-ястепень которого равна  (
( - натуральное число). Таким образом,
- натуральное число). Таким образом,  , если
, если  .
.
Если  - нечетное число, то выражение
- нечетное число, то выражение  имеет смысл при любом
имеет смысл при любом  ; если
; если  - четное число, то выражение
- четное число, то выражение  имеет смысл при
имеет смысл при 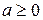 и не имеет смысла при
и не имеет смысла при  (четная степень любого действительного числа неотрицательна).
(четная степень любого действительного числа неотрицательна).
Пусть 
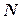
 тогда справедливы следующие свойства корня
тогда справедливы следующие свойства корня
1. 
| 5. 
|
2. 
| 6. 
|
3. 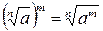
| 7. 
|
4.  , если , если 
| 8. 
|
Пример 3.1. Вычислить:
1) 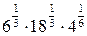 ; 2)
; 2) 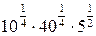 ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5)  .
.
Решение.
1) 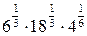
 ;
;
2)  ;
;
3)  ;
;
4) 

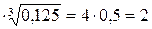 ;
;
5) 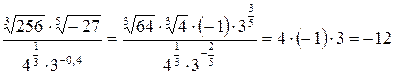 .
.
Ответ: 1) 6; 2) 10; 3) 4; 4) 2; 5)  .
.
Дата добавления: 2015-07-10; просмотров: 111 | Нарушение авторских прав