Читайте также:
|
Определение 3.8. Алгебраическим выражением называется выражение, составленное из чисел и переменных, знаков действия над ними (сложения, вычитания, умножения, деления, возведения в степень с рациональным показателем, извлечения арифметического корня) и скобок.
Два выражения называют тождественно равными, если при всех допустимых для них значениях переменных соответственные значения этих выражений равны. Замену одного выражения другим, тождественно равным ему выражением, называют тождественным преобразованием выражения.
Различают целые рациональные, дробные рациональные и иррациональные выражения. К целым рациональным выражениям относят одночлены и многочлены. Способы их преобразования были рассмотрены в пункте 3.2.
При тождественных преобразованиях дробных рациональных выражений (то есть содержащих деление на выражение с переменной) используются следующие основные приемы.
1. Сокращение дробей, основанное на свойстве дроби: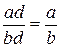 
. Например,
, (
).
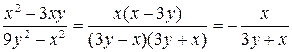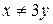2. Приведение к общему знаменателю – для этого необходимо:
1) разложить знаменатель каждой дроби на множители;
2) составить наименьший общий знаменатель;
3) домножив числитель и знаменатель каждой дроби на дополнительные множители, привести их к общему знаменателю.
Напомним, что действия над алгебраическими дробями осуществляются следующим образом
, 
, 
.
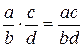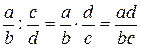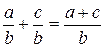Пример 3.12. Упростить выражение
.
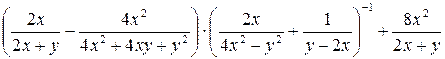Дата добавления: 2015-07-10; просмотров: 150 | Нарушение авторских прав