
Читайте также:
|
Пусть требуется разделить многочлен 
на двучлен  . Обозначим частное от деления как многочлен
. Обозначим частное от деления как многочлен
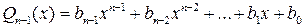 ,
,
а остаток - 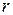 . Значение
. Значение 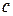 , коэффициенты многочленов
, коэффициенты многочленов  ,
,  и остаток
и остаток 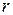 запишем в следующей форме:
запишем в следующей форме:

| 
| 
| … | 
| 
| |
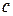
| 
| 
| 
| 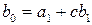
| 
|
В этой схеме каждый из коэффициентов  ,
,  , …,
, …,  получается из предыдущего числа нижней строки умножением на число
получается из предыдущего числа нижней строки умножением на число 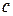 и прибавлением к полученному результату соответствующего числа верхней строки, стоящего над искомым коэффициентом. Если какая-либо степень
и прибавлением к полученному результату соответствующего числа верхней строки, стоящего над искомым коэффициентом. Если какая-либо степень  в многочлене отсутствует, то соответствующий коэффициент равен нулю. Определив коэффициенты по приведенной схеме, записываем частное
в многочлене отсутствует, то соответствующий коэффициент равен нулю. Определив коэффициенты по приведенной схеме, записываем частное
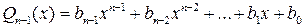
и результат деления, если  ,
,
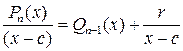 ,
,
или если  ,
,
 .
.
Теорема 3.1. Для того чтобы несократимая дробь 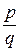 (
(
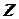 ,
, 
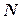 ) была корнем многочлена
) была корнем многочлена  с целыми коэффициентами, необходимо, чтобы число
с целыми коэффициентами, необходимо, чтобы число 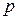 было делителем свободного члена
было делителем свободного члена  , а число
, а число 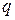 - делителем старшего коэффициента
- делителем старшего коэффициента  .
.
Теорема 3.2. (Теорема Безу) Остаток 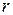 от деления многочлена
от деления многочлена  на двучлен
на двучлен 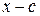 равен значению многочлена
равен значению многочлена  при
при  , то есть
, то есть  .
.
При делении многочлена  на двучлен
на двучлен 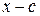 имеем равенство
имеем равенство
 .
.
Оно справедливо, в частности, при  , то есть
, то есть  .
.
Пример 3.2. Разделить 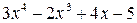 на
на  .
.
Решение. Применим схему Горнера:

| 
| 
| 
| 
| |

| 
| 
| 
| 
| 
|
Следовательно,
 ,
,
или  .
.
Пример 3.3. Разделить 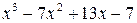 на
на  .
.
Решение. Применим схему Горнера:

| 
| 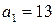
| 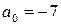
| |
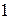
| 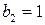
| 
| 
| 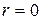
|
Следовательно,
 ,
,
или  .
.
Пример 3.4. Разделить  на
на  .
.
Решение. Проведем деление многочленов столбиком:




В итоге получаем

 .
.
Пример 3.5. Разделить  на
на  .
.
Решение. Проведем деление многочленов столбиком:



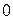
|
Тогда получаем

 .
.
Иногда бывает полезным представление многочлена в виде равного ему произведения двух или нескольких многочленом. Такое тождественное преобразование называют разложением многочлена на множители. Рассмотрим основные способы такого разложения.
Вынесение общего множителя за скобки. Для того чтобы разложить многочлен на множители способом вынесения общего множителя за скобки, необходимо:
1) найти общий множитель. Для этого, если все коэффициенты многочлена – целые числа, в качестве коэффициента общего множителя рассматривают наибольший по модулю общий делитель всех коэффициентов многочлена, а каждую переменную, входящую во все члены многочлена, берут с наибольшем показателем, который она имеет в данном многочлене;
2) найти частное от деления данного многочлена на общий множитель;
3) записать произведение общего множителя и полученного частного.
Группировка членов. При разложении многочлена на множители способом группировки его члены разбиваются на две или более групп с таким расчетом, чтобы каждую из них можно было преобразовать в произведение, и полученные произведения имели бы общий множитель. После этого применяется способ вынесения за скобки общего множителя вновь преобразованных членов.
Применение формул сокращенного умножения. В тех случаях, когда многочлен, подлежащий разложениюна множители, имеет вид правой части какой-либо формулы сокращенного умножения, его разложение на множители достигается применением соответствующей формулы, записанной в другом порядке.
Пусть 
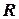 , тогда справедливы следующие формулы сокращенного умножения:
, тогда справедливы следующие формулы сокращенного умножения:

| 
|

| 
|

| 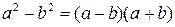
|

| 
|
Для  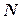 : : 
| |
Если  нечетное ( нечетное ( 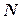 ): ): 
| |
Бином Ньютона:
 ,
где ,
где  - число сочетаний из - число сочетаний из  по по 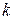 . .
|
Введение новых вспомогательных членов. Данный способ заключается в том, что многочлен заменяется другим многочленом, тождественно равным ему, но содержащим другое число членов, путем введения двух противоположных членов или замены какого-либо члена тождественно равной ему суммой подобных одночленов. Замена производится с таким расчетом, чтобы к полученному многочлену можно было применить способ группировки членов.
Пример 3.6. Разложить на множители многочлен  .
.
Решение. Все члены многочлена содержат общий множитель 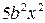 . Следовательно,
. Следовательно,  .
.
Ответ:  .
.
Пример 3.7. Разложить на множители многочлен  .
.
Решение. Группируем отдельно члены, содержащие коэффициент  , и члены, содержащие
, и члены, содержащие 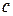 . Вынося за скобки общие множители групп, получаем:
. Вынося за скобки общие множители групп, получаем:


 .
.
Ответ:  .
.
Пример 3.8. Разложить на множители многочлен  .
.
Решение. Используя соответствующую формулу сокращенного умножения, получаем:
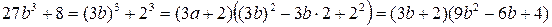 .
.
Ответ:  .
.
Пример 3.9. Разложить на множители многочлен  .
.
Решение. Используя способ группировки и соответствующую формулу сокращенного умножения, получаем:


 .
.
Ответ:  .
.
Пример 3.10. Разложить на множители многочлен 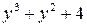 .
.
Решение. Заменим  на
на  , сгруппируем члены, применим формулы сокращенного умножения:
, сгруппируем члены, применим формулы сокращенного умножения:


 .
.
Ответ:  .
.
Пример 3.11. Разложить на множители многочлен
 .
.
Решение. Так как 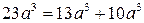 ,
, 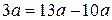 ,
,  , то
, то

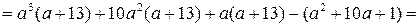
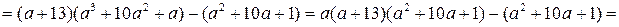
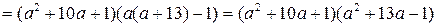 .
.
Ответ:  .
.
Дата добавления: 2015-07-10; просмотров: 136 | Нарушение авторских прав