Решение.

, ().

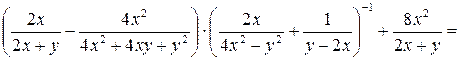
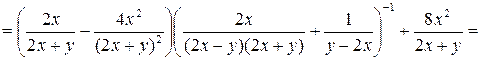
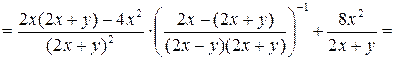
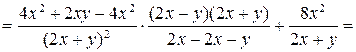
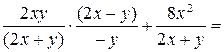
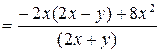
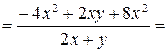
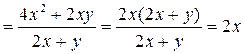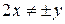Ответ: ,().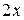

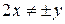Пример 3.13. Упростить выражение

.

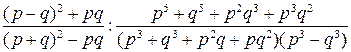Решение.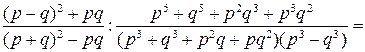

, (, ).

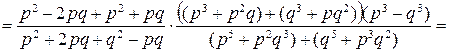
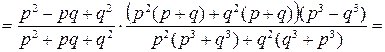
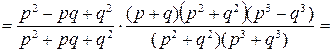
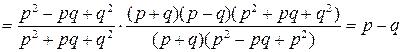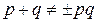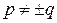Ответ: ,(, ).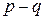

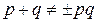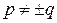Рассмотрим далее преобразование иррациональных выражений. Выражение называется иррациональным, если оно содержит извлечение корня из переменной или возведение переменной в дробную степень. Как правило, тождественные преобразования выполняются на множестве неотрицательных чисел. При решении примеров мы будем это подразумевать и специально не оговаривать.

Пример 3.14. Упростить выражение .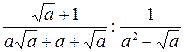

Решение.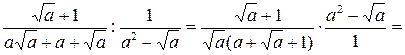

.

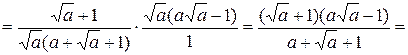
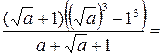
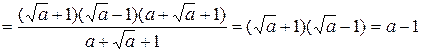Ответ: .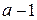

Пример 3.15. Упростить выражение .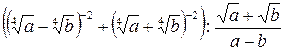

Решение.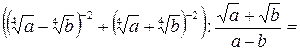

.

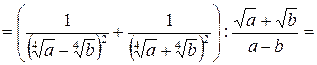
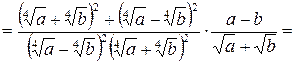
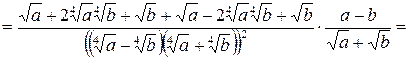
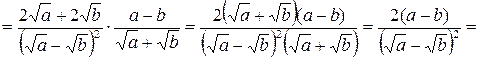
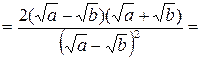
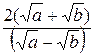Избавимся от иррациональности в знаменателе. Для этого домножим числитель и знаменатель на выражение, сопряженной к знаменателю, то есть на сумму 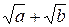. Получим

.

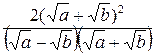
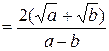Ответ: .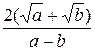

Пример 3.16. Упростить выражение

.

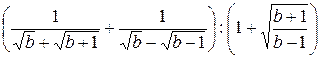Решение. Избавимся от иррациональности в знаменателе каждой из дробей в первой скобке:

,

.

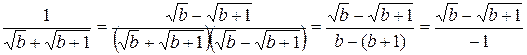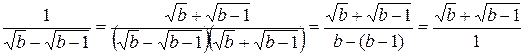Подстановка полученных выражений дает

.

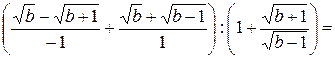
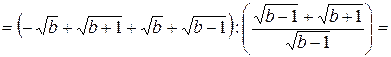
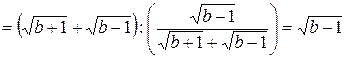Ответ: .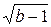

Пример 3.17. Упростить выражение

.

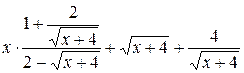Решение. Сделаем замену переменной 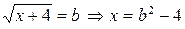. Тогда исходное выражение имеет вид

.

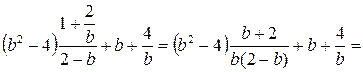
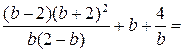
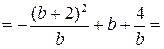
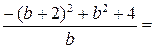
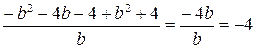Рассмотрим далее пример, содержащий произведение корней с различными показателями.

Ответ: .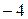

Пример 3.18. Упростить выражение .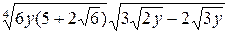

Решение.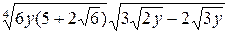

.

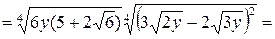
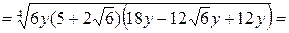
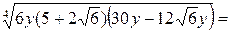
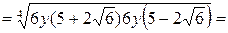
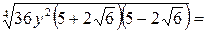
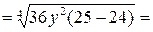
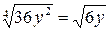Ответ: .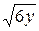

Пример 3.19. Вычислить .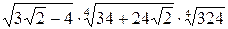

Решение. Заметим, что

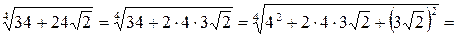
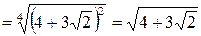, тогда

= .

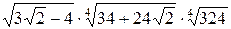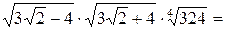
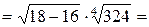
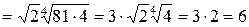Ответ: 6.

Пример 3.20. Вычислить .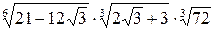

Решение. Так как 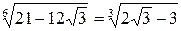, то

= .

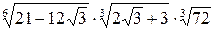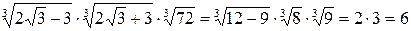Ответ: 6.

Пример 3.21. Вычислить .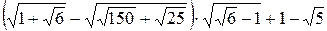

---

Дата добавления: 2015-07-10