
Читайте также:
|
Сумму и разность многочленов можно преобразовать в многочлен стандартного вида. При сложении двух многочленов записываются все их члены и приводятся подобные члены. При вычитании знаки всех членов вычитаемого многочлена меняются на противоположные.
Например:
 ,
,
 .
.
Члены многочлена можно разбивать на группы и заключать в скобки. Поскольку это тождественное преобразование, обратное раскрытию скобок, то устанавливается следующее правило заключения в скобки: если перед скобками ставится знак «плюс», то все члены, заключаемые в скобки, записывают с их знаками; если перед скобками ставится знак «минус», то все члены, заключаемые в скобки, записывают с противоположными знаками.
Например,
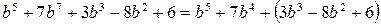 ,
,
 .
.
Правило умножения многочлена на многочлен: чтобы умножить многочлен на многочлен, достаточно каждый член одного многочлена умножить на каждый член другого многочлена и полученные произведения сложить.
Например,

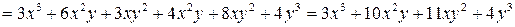 .
.
Итак, многочлены можно складывать, вычитать и умножать. При этом в результате снова получится многочлен.
Определение 3.6. Многочленом от одной переменной  степени
степени  называют выражение вида
называют выражение вида
 ,
,
где 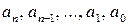 - любые числа, которые называют коэффициентами многочлена, причем
- любые числа, которые называют коэффициентами многочлена, причем 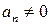 ,
,  - целое неотрицательное число.
- целое неотрицательное число.
Если 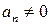 , то коэффициент
, то коэффициент  называют старшим коэффициентом многочлена
называют старшим коэффициентом многочлена  , одночлен
, одночлен  - его старшим членом, коэффициент
- его старшим членом, коэффициент  - свободным членом.
- свободным членом.
Если вместо переменной  в многочлен
в многочлен  подставить действительное число
подставить действительное число 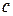 , то в результате получится действительное число
, то в результате получится действительное число  , которое называют значением многочлена
, которое называют значением многочлена  при
при  .
.
Определение 3.7. Число 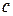 называют корнем многочлена
называют корнем многочлена  , если
, если  .
.
Рассмотрим деление многочлена  на многочлен
на многочлен  , где
, где 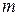 и
и  - натуральные числа. Деление возможно, если степень многочлена-делимого
- натуральные числа. Деление возможно, если степень многочлена-делимого  не меньше степени многочлена-делителя
не меньше степени многочлена-делителя  , то есть
, то есть 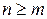 .
.
Разделить многочлен  на многочлен
на многочлен  ,
, 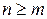 , - значит найти два таких многочлена
, - значит найти два таких многочлена 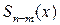 и
и  , чтобы
, чтобы
 .
.
При этом многочлен 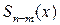 степени
степени  называют многочленом-частным,
называют многочленом-частным,  - остатком,
- остатком,  .
.
Замечание 3.2. Если делитель  - не нуль-многочлен, то деление
- не нуль-многочлен, то деление  на
на  ,
, 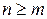 , всегда выполнено, а частное и остаток определяются однозначно.
, всегда выполнено, а частное и остаток определяются однозначно.
Замечание 3.3. В случае, когда 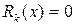 при всех
при всех  , то есть
, то есть
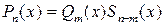 ,
,
говорят, что многочлен  нацело делится (или делится) на многочлен
нацело делится (или делится) на многочлен  .
.
Деление многочленов выполняется аналогично делению многозначных чисел: сначала старший член многочлена-делимого делят на старший член многочлена-делителя, затем частное от деления этих членов, которое будет старшим членом многочлена-частного, умножают на многочлен-делитель и полученное произведение вычитают из многочлена-делимого. В результате получают многочлен – первый остаток, который делят на многочлен-делитель аналогичным образом и находят второй член многочлена-частного. Этот процесс продолжают до тех пор, пока получится нулевой остаток или степень многочлена остатка будет меньше степени многочлена-делителя.
При делении многочлена на двучлен можно воспользоваться схемой Горнера.
Дата добавления: 2015-07-10; просмотров: 101 | Нарушение авторских прав