|
Читайте также: |
Если известен график функции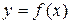 
, то с помощью некоторых преобразований плоскости (параллельного переноса, осевой и центральной симметрии и т. п.) можно построить графики более сложных функций.
1. График функции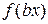 
получается сжатием графика функции 
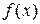в 
раз к ос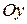и 
при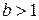 
или растяжением в 
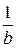раз от этой оси 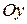при 
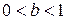(рисунок 2.12).
|
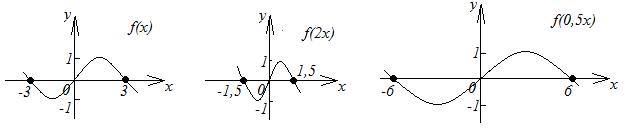
| рис. 2.12 |
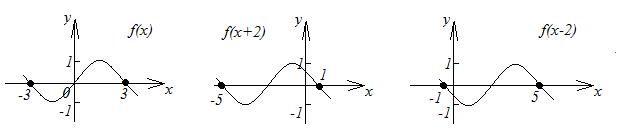
2. График функции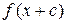 
получается параллельным переносом графика 
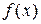в отрицательном направлении оси 
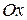на 
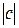при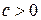 
и в положительном направлении на 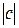при 
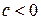(рисунок 2.13).
|
| рис. 2.13 |
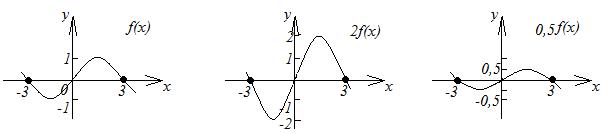
3. График функции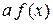 
получается растяжением графика функции 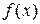вдоль оси 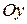в 
раз при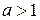 
и сжатием вдоль этой оси в 
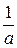раз при 
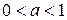(рисунок 2.14).
|
| рис. 2.14 |
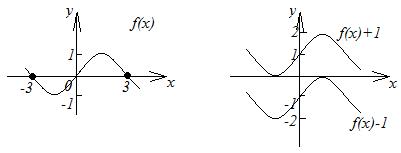
4. График функции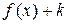 
получается параллельным переносом графика 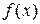в положительном направлении оси 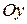на 
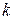при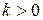 
и в отрицательном направлении этой оси на 
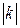при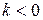 
(рисунок 2.15).
| 
|
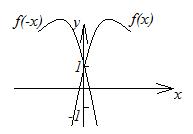
| рис. 2.15 | рис. 2.16 |
5. График функции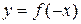 
получается симметричным отображением графика 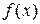относительно оси 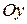(рисунок 2.16).
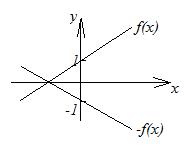
6. График функции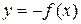 
получается симметричным отображением графика 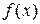относительно оси 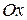(рисунок 2.17).
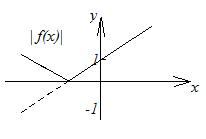
7. График функции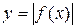 
получается из графика функции 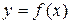следующим образом: часть графика 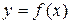, лежащая над осью 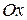, сохраняется, часть его, лежащая под осью 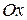, отображается симметрично относительно оси 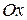(рисунок 2.18).
| 
| 
|
| рис. 2.17 | рис. 2.18 | рис. 2.19 |
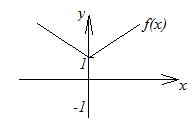
8. График функции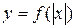 
получается из графика функции 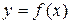следующим образом: часть графика функции 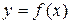следующим образом: при 
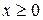график 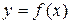сохраняется, а при 
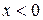полученная часть графика отображается симметрично относительно оси 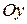(рисунок 2.19).
Дата добавления: 2015-07-10; просмотров: 116 | Нарушение авторских прав