Процессы размножения и гибели. Поток Эрланга.

Процессы размножения и гибели – разновидность непрерывных марковских цепей, у которых граф состояний и переходов имеет вид:

Все состояния вытянуты в цепочку, в которой каждая из средних связана прямо и обратной связью с каждым из соседних.

В стационарном режиме:

S1:P1λ12=P2 λ21 S2: P2 λ21+P2 λ23=P1 λ12+P3 λ32

Предельная вероятность P1:

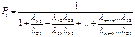
Поток Эрланга:

Эрланговский поток событий – последовательность заявок, получаемая из пуассоновского потока, путем выполнения операции просеивания. Используется параметр – порядок закона Эрланга(k).

Если k=3, то из пуассоновского потока выбирается каждое 3-е событие, и формируется поток Эрланга 3 порядка. Простейший поток – частный случай потока Эрланга, а именно поток Эрланга 1 порядка.

Количественные характеристики:

1. Мат. ожидание

2. Интенсивность потока Эрланга

3. Дисперсия

4. Среднее отклонение

Дата добавления: 2015-10-21