Простейший поток событий. Пуассоновский поток.

Свойства потоков:

Стационарность – поток называется стационарным, если вероятность появления того или иного числа событий на элементарном участке τ, зависит только от его длины, и не зависит от того, где он расположен на временной оси. Стационарность обозначает однородность времени.

Отсутствие последействия – поток называется потоком без последействия, если для любых непересекающихся участков времени число событий на одном не зависит от числа событий на другом.

Ординарность – поток событий называется ординарным, если вероятность попадания 2-х или более событий на элементарный участок пренебрежимо мало, по сравнению с вероятностью попадания одного события.

Пуассоновский поток – поток, не имеющий последействия и ординарен.

Число событий, попадающих на любой участок распределено по закону Пуассона. Вероятность попадания k событий на участок τ задается формулой Пуассона: , где a – среднее число событий на τ, для стационарного потока a=λτ.

Характеристика потока:

1. Закон распределения случайной величины Т – интервалы емжду соседними событиями в потоке F(t)=P(T<t), вероятность того, что на t попадет хотябы 1 событие F(t)=1-P₀; P₀=e^-λτ/

2. Числовые характеристики:

a. Мат. ожидание

b. Дисперсия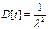

c. Среднеквадратическое отклонение

Дата добавления: 2015-10-21