Марковские случайные процессы. Эргодические цепи Маркова

Марковские процессы (процессы без последействия) – разновидность случайных процессов, описывающих систему с дискретными состояниями: если система в момент n находится в состоянии j, то вероятность её перехода в момент n+1 в состояние k зависит только лишь от значений n,j,k и не зависит от того, в каких состояниях система была в более раннее, чем n моменты времени.

Пространство состояний представляет собой конечное счетное множество, часто отождествляемое с множеством целых неотрицательных чисел.

Дискретный Марковский процесс с дискретным временем называется дискретной цепью Маркова. Он характеризуется тем, что переходы возможны лишь в дискретные моменты времени t₀,t₁,t₂.

В Марковском процессе с непрерывным временем, переход возможен в любой, наперед неизвестный момент времени.

Цель Марковских процессов описывается матрицей переходов за 1 шаг:

где P_ij – вероятность перехода за один шаг из состояния z_i в z_j. Марковская цепь однородна, если P_ij не зависит от шага.

Равенство Маркова (реккурентная формула для определения вероятностей состояния системы после k-ого шага, через вероятность после k-1):

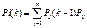
Свойства эргодической цепи Маркова:

Эргодическое состояние – если возвратное состояние не является ни нулевым, ни периодическим. Вероятность того что система когда-нибудь вернется в состояние j:

Если f_j=1, то j – возвратное состояние, а если f_j<1, то j – невозвратное состояние.

Также различают при fj=1: если среднее время между пребываниями системы в состоянии стремится в бесконечность, то состояние j – возвратное ненулевое, если это время конечная величина, то j – возвратное нулевое

Если ||P_ij|| - не содержит нулевых элементов, для такой цели характерно то, что при большом числе шагов n->бесконечности, наступает стационарный режим.

Предельная вероятность нахождения в состоянии j:

Дата добавления: 2015-10-21