Устройство декодирования для режима исправления ошибок

Всякому исправляемому вектору ошибок соответствует свой синдром, т.е.

" e_i(x),e_j(x)ÎE e_i(x)¹e_j(x) ® S_i(x)=Rem[e_i(х)/g(x)]¹S_j(x)=Rem[e_j(х)/g(x)].

Из этого следует, что между элементами множества ошибок Е и элементами множества синдромов S (в разд. 4 синдром имел обозначение D) установлено взаимно однозначное соответствие.

Существуют два метода определения полинома ошибок по синдрому - параллельный и последовательный методы.

6.2.1. Параллельный метод определения ошибок. Схема кодера, работающего согласно параллельному методу, приведена на рис.5.12.

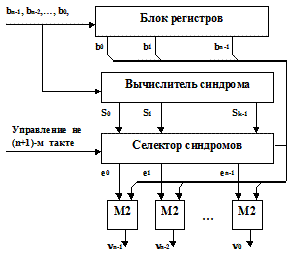
Рис.5.12

Рассмотрим пример. Для циклического кода заданы: n=5, m=2, d=3, g(x)=x³+x²+1, r=s=1, |Е|=5. Множество полиномов ошибок Е={х⁴, х³, х², х¹, х⁰}. Множество полиномов синдромом ошибок S={х²+х+1, х²+1, х², х, 1}.

Вычислитель синдрома представляет собой такую же схему, как и вычислитель синдрома на рис.5.11. Схема селектора синдромов (см. рис.5.12) представляет собой комбинаторную схему, синтезированную согласно таблице соответствия элементов множества синдромов S множеству ошибок Е. Соответствие для данного примера приведено в табл.5.9.

Исходя из данных табл.5.9, синтезирована схема селектора синдромов, вид которой приведен на рис.5.13. Следует отметить, что сложность селектора синдрома определяется длиной кода и числом исправляемых ошибок |Е|.

Таблица 5.9

S	Е
S2	S1	S0	e4	e3	e2	е1	е0

Рис.5.13

6.2.2. Последовательный метод определения ошибок. Данный метод направлен на сокращение числа синдромов и упрощение реализации. Логика метода изложена в разд.4.3.

На рис.5.14 приведена схема декодера, в которой процедура декодирования осуществляется за 2n тактов. Первые n тактов осуществляется определение синдрома ошибки принятой кодовой комбинации, а последние n тактов определяется разряд кодовой комбинации, содержащий ошибку.

Рис.5.14

Схема селекции настроена на синдром ошибки старшего разряда. В течение первых n тактов ключ К1 находится в положении 2, ключ К2 замкнут. Происходит определение синдрома ошибки принятой кодовой комбинации.

В течение последующих n тактов ключ К1 переводится в положение 1, а ключ К2 разомкнут. Начат этап исправления ошибки. В первые n тактов заполняется блок регистров и в вычислителе синдрома определяется синдром ошибки старшего разряда. В течение последующих n тактов осуществляется циклический сдвиг и выполняется поиск ошибки так, как это описано в разд. 4.3. На (2n+1)-ом такте подается сигнал разрешения на выдачу исправленной кодовой комбинации. Реализацию и работу схемы селекции рассмотрим на примере последующего декодера (см. рис.5.15).

Недостатком данной схемы является задержка при декодировании на n тактов.

Избавиться от данного недостатка позволяет применение декодера, схема которого приведена на рис.5.15.

Рис.5.15

Работает декодер при непрерывной передаче следующим образом.

Информация записывается одновременно в первый буферный регистр БР1 и в первый вычислитель синдрома ВС1. В ВС1 происходит определение синдрома ошибки в принятой комбинации циклического кода. Между n -ым и (2n+1)-ым тактами содержимое ВС1 переносится во второй вычислитель синдрома ВС2. Содержимое ВС1 сбрасывается в ноль. В последующие n+1 тактов в ВС2 происходит циклический сдвиг найденного в ВС1 синдрома. Схема селекции представляет собой селектор нулевого синдрома (см. рис.5.10 и рис.5.11). Исправленная кодовая комбинация записывается во второй буферный регистр БР2.

Так как этап исправления ошибок в b^*(х) совпадает с этапом вычисления синдрома последующей кодовой комбинации, то импульсы считывания информации на элементы И поступают через каждые n тактов. На рис.5.16 приведены временные диаграммы, показывающие последовательность приема кодовых комбинаций, вычисления синдрома ошибок и выдачи информации получателю.

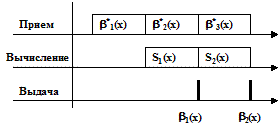
Рис.5.16

Пример. Для циклического кода заданы: n=6, m=3, d=3, g(x)=x³+x²+1, r=s=1. Схема декодера при непрерывной передаче приведена на рис.5.17. Селектор синдрома настроен на корректор ошибки старшего разряда S₆(х)=х+1 (011).

Пусть b*(х)=b(х)Åe(x)=(х⁵+х⁴+х²)Åх⁴=х⁵+ х². Работа декодера отображена в виде временных диаграмм, приведенных в табл.5.10.

Рис.5.17

Таблица 5.10

№	Код	ВС1	ВС2	СС
		D01	D11	D21	D02	D12	D22

Окончание табл. 5.10

№	Регистр	М2
	D01	D11	…	D51

Дата добавления: 2015-10-21