Коды по законам комбинаторики

Способы комбинирования позволяют строить комбинаторные коды. Различают коды, использующие все возможные комбинации с их частичным использованием [11].

1.2.1. Коды по закону размещений. Закон соединений предусматривает, что кодовая комбинация включает n символов из их общего числа k. Длина кодовой комбинации может быть 2£n£k-1. Комбинации различаются либо составом символов, либо порядком их следования.

Мощность кода определится по формуле

.

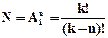Пример. Пусть k =4, k={0,1,2,3}, N= 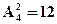. Построить код по закону размещений.

Множество кодовых комбинаций {01, 02, 03, 12, 13, 23, 10, 20, 30, 21, 31, 32}.

1.2.2. Коды по закону сочетаний. Закон соединений определяет построение кодовых комбинаций с включением в них n символов из К в алфавите. Кодовые комбинации различается только составом символов.

Мощность кода определится по формуле

.

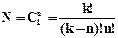Пример. Пусть k =4, k={0,1,2,3}, n=2 .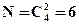

Множество кодовых комбинаций {01, 01, 03, 12, 13, 23} или {10, 20, 30, 21, 31, 32}.

1.2.3. Коды по закону перестановок. Закон перестановок характеризуется тем, что все k символов алфавита однократно входят в каждую кодовую комбинацию, т.е. n = k. Кодовые комбинации различаются порядком следования символов. Мощность кода определится по формуле N=P_K=k!.

Пример. Пусть k =3, k={0,1,2}, N=P_K=3!=6.

Множество кодовых комбинаций {012, 021, 102, 120, 201, 210}.

Очевидно, что для данного кода с ростом N необходимо очень быстро увеличивать k. Это недостаток кода.

Уменьшить алфавит кода при заданном числе N можно за счет увеличения длины кодовой комбинации, т.е. r –кратного повторения одного или нескольких символов в кодовой комбинации.

Пусть каждая кодовая комбинация содержит r_i число символов i, тогда мощность кода определится по формуле

.

Данный код называется кодом по закону перестановок с повторением.

Пример. Пусть k =3, k={0,1,2}, r₀=2, r₁=r₁=1, N=12.

Множество кодовых комбинаций {0012, 0021, 0102, 0120, 0201, 0210, 1002, 1020, 1200, 2001, 2010, 2100}.

1.2.4. Сменно–качественные коды. Это разновидность кодов на соединения. В данных кодах соседние символы не должны быть одинаковы. Основание должно быть k>2. Если k=2, то получим при n=4 только две кодовые комбинации 0101 и 1010. Мощность кода определится по формуле N=k(k-1)^n-1.

Пример. Пусть k =3, n=3, N=3x2²=12.

Множество кодовых комбинаций {010, 012, 020, 021, 101, 102, 120, 121, 201, 202, 212, 210}.

Дата добавления: 2015-10-21