Методы кодирования циклических кодов

Известны три метода кодирования и соответственно три способа построения кодирующих устройств, первые два из которых основаны на свойствах порождающего полинома [11].

5.2.1. Модель 1. Согласно правилу (4.1), комбинация циклического кода b(х) может быть получена при умножении комбинации простого кода n(х) на образующий полином g(х). На этом правиле и построено кодирующее устройство, т.е. оно представляет собой устройство умножения (см. рис.5.1).

Это устройство является простым в реализации, но его недостаток состоит в том, что получаемый циклический код не является систематическим. Принятая кодовая комбинация в явном виде не содержит информационных символов. Для выделения информационных символов следует дополнительно, после приема, выполнять операцию деления b(х)/g(x)=n(x), что усложняет приемник.

5.2.2. Модель 2. Данная модель предусматривает вычисление остатка r(x) от деления информационного полинома n(х), предварительно умноженного на х^k, на порождающий полином, т.е.

n(х)х^k=g(x)g^’(x)År(х). (5.1)

Рассмотрим полином b(х)=g(x)g^’(x)=n(х)х^kÅr(х)=n(х)х^kÅr(х) по модулю (хⁿ+1). Коэффициенты при n-k старших разрядах рассматриваются как m информационных символов, а при k младших расположены проверочные символы. Следовательно, полученный код будет систематическим (см. правило (4.2)).

При построении кодера используют одновременно операции умножения на n(х)=х^k и деления на g(x).

Схема устройства автоматического кодирования приведена на рис.5.6.

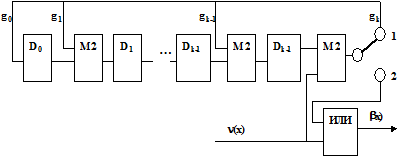
Рис.5.6

В течение первых m тактов ключ находится в положении 1. Коэффициенты безызбыточного кода n(х) через элемент ИЛИ поступают на выход устройства и через полусумматор – в схему автоматического умножения на n(х)=х^k и деления на g(x). В элементах памяти D_i к концу m -го такта будет сформирован остаток от n(х)х^k/g(x)=r(x).

Между m и (m+1) -м тактами ключ переводят в положение 2, обратная связь разрывается. Выход полусумматора подключается ко входу элемента ИЛИ и содержимое (r(x)) регистра на элементах памяти D_i выталкивается на выход кодера.

Пример. Построить кодер для кода (7,4) при g(x)=x³+x²+1, m =4, k =3. Схема устройства приведена на рис.5.7.

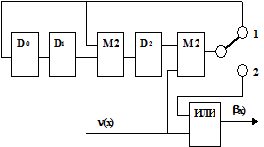
Рис.5.7

Полином безызбыточного кода имеет вид n(х)=x³+x+1, полином циклического кода b(х)=x⁶+x⁴+x³+x².

Можно убедиться, что r(x)=x².

В табл.5.5 приведены временные диаграммы работы кодера.

Таблица 5.5

Такты	Ключ	Вход	D0	D1	M2	D2	M2	Выход

К концу четвертого такта в элементах памяти D_i сформирован остаток x². Действительно, элемент D₂ находится в состоянии “единица”, а остальные элементы памяти - в состояниях “ноль”.

5.2.3. Модель 3. Данная модель основана на свойствах проверочного полинома.

Из разд.4 известно, что

b(х)h(x)º0 по mod (xⁿ+1). (5.2)

Пусть (bH⁽ⁱ⁾), i=1,2,…,n-1 - скалярное произведение, где H⁽ⁱ⁾ – вектор, коэффициенты которого сдвинуты на i разрядов в сторону старшего разряда (влево). Вектор b ортогонален вектору H, записанному в обратном порядке, и всем векторам, образованным циклическим сдвигом.

Если информационные символы размещены на первых m позициях кодового вектора b(х), то с помощью первых k уравнений системы (5.2) можно определить контрольные символы.

Рассмотрим уравнение

(bH⁽⁰⁾)=0=(b_n-1,b_n-2,…,b₀)(h₀,h₁,…,h_m,0_m+1,…,0_n-1)=0,

причем число нулей равно k:

b_n-1h₀Å b_n-2h₁Åb_n-3h₂Å …Å b_n-mh_m-1Å b_n-m-1h_m=0.

Заметим, что b_n-1h₀ – это элемент n_m-1, b_n-2h₁ – это элемент n_m-2, b_n-mh_m-1 – элемент n₀, а b_n-m-1h_m - это первый неизвестный контрольный символ.

Так как h_m, то b_n-m-1= b_n-1h₀Å b_n-2h₁Åb_n-3h₂Å …Å b_n-mh_m-1= ,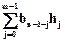

(bH⁽¹⁾)=0=(b_n-1,b_n-2,…,b₀)(0,h₀,h₁,…,h_m,0,…,0)=0,

причем число нулей равно k-1.

В общем случае (bH⁽⁰⁾)=0 " i=1,2,…kб

b_n-m-ш= 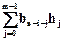. (5.3)

По формуле (5.3) находятся все контрольные символы, а получаемый циклический код будет систематическим.

Схема кодера приведена на рис.5.8

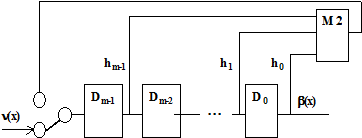
Рис.5.8

При построении схемы следует выполнять условия:

- число ячеек памяти равно deg[h(x)];

- если коэффициент h_i=1, то выход ячейки D_i соединен со входом полусумматора М2, а если коэффициент h_i=0, то выход ячейки D_i соединен со входом ячейки D_i-1.

Работает кодер следующим образом.

Первые m тактов ключ находится в положении 1, затем между m –м и (m+1)-м тактом переводится в положение 2. В положении 2 ключ находится k тактов, а затем снова переводится в положении 1. Таким образом, в течение m тактов заполняется регистр из D - триггеров, а затем вычисляются контрольные символы.

Недостаток данной схемы обусловлен задержкой на m тактов.

Пример. Пусть проверочный полином h(x) кода (7.4) имеет вид h(x)=x⁴+x³+x²+1, последовательность безызбыточного кода n=1100, комбинация циклического кода b=1100101.

Схема кодера приведена на рис.5.9. В табл.5.6 приведены временные диаграммы, поясняющие работу кодера при кодировании n=1100.

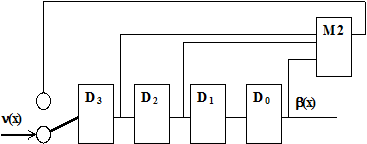
Рис.5.9

Таблица 5.6

Ключ	Такты	n(х)	D3	D2	D1	D0	M2	Выход

Дата добавления: 2015-10-21