Условия обнаружения и исправления ошибок

Для исправления ошибок необходимо, чтобы различным ошибкам соответствовали различные значения синдрома, т.е

.

Отметим еще одно свойство проверочной матрицы. Групповой код имеет минимальное кодовое расстояние d, если любые d-1 или менее столбцов проверочной матрицы линейно независимы. Произведение (3.8) представим в виде

, (3.10)

где e_i - компонент вектора ошибки, h_i - i -й столбец проверочной матрицы, e_i´h_i - произведение скаляра e_i на матрицу-строку h_i.

Следовательно, для обнаружения ошибок кратности d-1 и менее необходимо и достаточно, чтобы d-1 или менее столбцов проверочной матрицы были линейно независимыми.

Из условия (3.10) следует, что опознаватель ошибок можно получить поразрядным сложением тех столбцов h_i проверочной матрицы, которым соответствуют единицы на позициях комбинации ошибок.

Поскольку опознаватель одиночных ошибок содержит только одну единицу, то состав столбцов проверочной матрицы приобретает следующий смысл. В столбцах h_i проверочной матрицы записаны опознаватели одиночных ошибок, имеющих место в i -м разряде кодовой комбинации.

Применяя условия (3.8), (3.9) и (3.10), можно построить все возможные формы опознавателей обнаруживаемых и исправляемых кодом ошибок, которые сводятся в таблицу, называемую таблицей декодирования.

Поскольку получателю выдаются информационные разряды, то исправление ошибок в контрольных разрядах не производится.

Пример построения групповых кодов. Построить код для передачи 25 сообщений, который будет обнаруживать и исправлять одну ошибку.

При М =27 m =5, s =1, r =1, d =3. Число контрольных разрядов k =4.

Образующая и проверочная матрицы имеют вид

, .

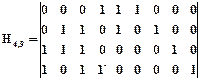Вид таблицы декодирования приведен в табл.5.1

Дата добавления: 2015-10-21