Расчет статически неопределимого круглого вала работающего на кручение

Решение:

Схема нагружения стержня представлена на рисунке. Освобождаем стержень от связей, заменяем их моментами в заделках - МА и МD
Условием равновесия стержня является только одно

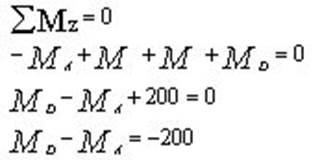
Как видно, уравнение содержит две неизвестные. Задача является один раз статически неопределимой.
Дополнительное уравнение составим, рассматривая геометрическую сторону задачи. Условия деформации стержня состоят в том, что угол закручивания концевых сечений А и D равен нулю, т.е. .
Угол закручивания сечения А или сечения В определяется как сумма углов закручивания отдельных участков стержня.
Определим значения крутящих моментов в сечениях стержня, рассматривая отсеченные правые части.
Сечениями, где приложены внешние моменты, стержень разбивается на три участка I, II, III.
В произвольном сечении на участке I: ,
на участке II: Мкр II =МD + М,
на участке III: Мкр III = МD + М + М
Угол закручивания сечения А или сечения D найдется как сумма углов закручивания отдельных участков стержня.
Определим значения крутящих моментов в сечениях стержня, рассматривая отсеченные правые части.
Углы закручивания на каждом участке запишутся на основании закона Гука

На участке DС:
На участке BD:
На участке AB:
Здесь Jp - полярные моменты инерции поперечных сечений вала.


Величины крутящих моментов на участках стержня равны:

По полученным значениям, строим эпюру крутящих моментов.
Диаметр стержня определим из условия прочности стержня при кручении
.
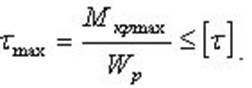Наибольшая величина крутящего момента Mкр max = 144 Hм на участке стержня АВ.

Построим эпюры углов закручивания и касательных напряжений.

Углы закручивания относительно неподвижного сечения

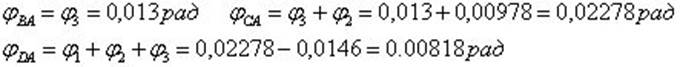
Определим наибольший момент.

Дата добавления: 2015-10-16