Изгиб с кручением круглых валов

Дано: N=26л.с.; n=360 об/мин; а=1.2м; в=0.6м; с=1.1м; D1=450cм; D2=400см; .

Решение:

1) Определение моментов, приложенных к шкивам. Момент на шкивах по передаваемой мощности и скорости вращения вала определяется по формуле
, где N - передаваемая валом мощность, Вт,
w– угловая скорость вращения вала, рад/с.
Угловую скорость можно вычислить по формуле
Вычисляем момент на первом шкиве:
Моменты на втором и третьем шкивах будут одинаковыми и равны половине момента первого шкива

Построим эпюры крутящих моментов.
2) Определение окружных усилий.

Спроектируем усилия P1 и P2 на координатные оси x и y:

3)Определяем силы, изгибающие вал в горизонтальной и вертикальной плоскостях, и строим эпюры изгибающих моментов.
Рассматриваем изгиб вала в плоскости ZOX.

Рассматриваем изгиб вала в плоскости YOZ.

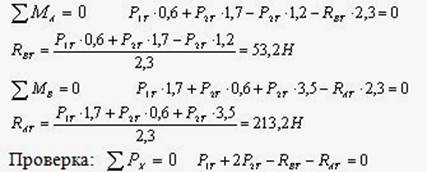
4) Построим эпюру суммарных изгибающих моментов
Находим суммарный момент по формуле:

5) Определение опасного сечения и величины максимального расчетного момента по третьей теории прочности.
Из эпюр Mk и Mu видно, что опасное сечение будет в точке C, где

5) Условие прочности вала по третьей теории прочности определяется по формуле
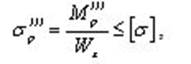, где Wx - осевой момент сопротивления сечения. Для круга:

Принимаем диаметр вала:

Дата добавления: 2015-10-16