Решение. Выбор сечения, расчет деформаций и напряжений стержня работающего на изгиб

Выбор сечения, расчет деформаций и напряжений стержня работающего на изгиб

Дано: q2=50кН/м; q3=40кН/м; F2 =20кН; М2=20кНм; L1=2м; L2=5м; L3=2м.

Решение

Схема нагружения балки представлена на рисунке. Определим опорные реакции, записывая уравнения моментов всех сил, приложенных к балке, относительно точек А и В.

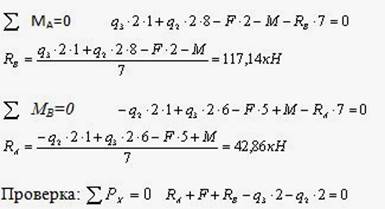
Положительные знаки опорных реакций свидетельствуют о том, что предполагаемое направление соответствует истинному. Возьмем на балке характерные сечения и вычислим в них величины Q и М.
Определение значений поперечной силы в характерных сечениях.

По найденным значениям поперечных сил построена эпюра Q
Определение величин изгибающих моментов в характерных сечениях.

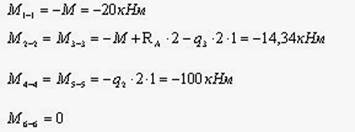
По найденным значениям моментов строим эпюру изгибающих моментов М.
2. Подбор поперечного сечения балки. Опасным является сечение B, где возникает наибольший по абсолютной величине Ммах = 100 кН×м. Двутавровое сечение балки подбираем из условия прочности при изгибе при расчетном сопротивлении материала 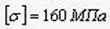(сталь):
.
Откуда требуемый момент сопротивления Wх равен:

По сортаменту (ГОСТ 8239-72) принимаем двутавр № 36 с Wx = 743 см3.

Опасное сечение в точке, где М=100кНм, Q=100кН.
Определим максимальные, нормальные напряжения

Максимальные касательные напряжения

Определяем эквивалентные напряжения в опасном сечении в точке С по формуле

Условие прочности выполняется.
Определим перемещение точек балки.
Граничные условия имеют следующий вид:

Жесткость балки
Зная значения начальных параметров вычислим правые части универсальных уравнений меняя координату х через каждые 0,5м



По полученным данным строим эпюры линейных перемещений и углов.

Дата добавления: 2015-10-16