Расчет рамы испытывающей динамические нагрузки

Дано: L=1,8м; а/L=0.4; Q=120кН; Р=1,2кН; е=0,028м; Двутавр №18; d=0,14м; Ls=1.8м; n=400об/мин.

Решение:

Вычислим реакции опор

Строим эпюру изгибающих моментов.
Определим статическое перемещение точки приложения груза (прогиб балки).

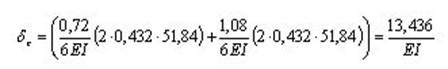
Двутавр №18
Подставим значения:

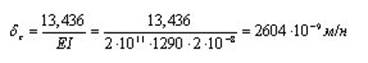
На самом деле, точка В за счет удлинения стержня ВD переместится на величину Это удлинение происходит под влиянием опорной реакции в точке В.

Из подобия треугольников
Полное вертикальное перемещение точки С будет равно

Частота свободных колебаний
Вертикальная составляющая центробежной силы S, представляет собой периодическую силу вызывающая поперечные колебания балки в вертикальной плоскости. Частота силы S(t)

Динамический коэффициент
Максимальное значение центробежной силы

Наибольший динамический прогиб балки в сечении где расположен двигатель, в точке С

Наибольший статический прогиб

Наибольший полный прогиб
Наибольшие динамические напряжения

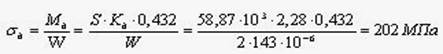
Наибольшие статические напряжения

Наибольшие полные напряжения условие прочности не выполняется, необходимо увеличить сечение балки
Двутавр №20


Наибольшие полные напряжения условие прочности выполняется, окончательно принимаем балку из двух двутавров
№20
Прогибы балки изменяются по закону

Напряжения изминяются по закону

Графики этих функций покажем на рисунке

Дата добавления: 2015-10-16