Теорема 2. При піднесенні обох частин рівняння до парного степеня отримане рівняння є наслідком даного. В якому можуть виникати сторонні корені, які відсіюються перевіркою.

Доведення. Покажемо, що рівняння

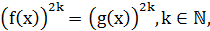(5)

є наслідком рівняння

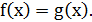(6)

Нехай числа α - корінь рівняння (6), тобто . Тоді

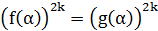. Отже, число α є коренем рівняння (5).

Ми показали, що кожен корінь рівняння (6) є коренем рівняння (5). Це означає, що рівняння (5) є наслідком рівняння (6).

Зауважимо, що коли число β - корінь рівняння (5), то з рівності 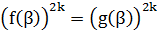не обов’язково випливає, що 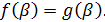Тому в результаті переходу від рівняння до наслідку 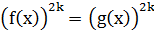можуть з’явитися сторонні корені, які можна виявити за допомогою перевірки.

Приклад 4. Розглянемо рівняння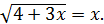

Розв’язання. Піднесемо обидві частини рівняння до квадрата, отримаємо рівняння, яке є наслідком даного:

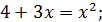
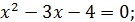
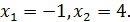
Перевірка показує, що число -1 є стороннім коренем, а число 4 задовольняє дане рівняння.

Відповідь: 4.

Приклад 5. Розглянемо рівняння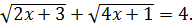

Розв’язання. Піднесемо обидві частини даного рівняння до квадрата:

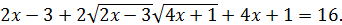
Звідси .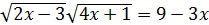

Переходячи до рівняння-наслідку, отримуємо:

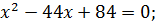
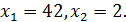
Перевіривши бачимо, що число 42 є стороннім коренем, а число 2 задовольняє дане рівняння.

Відповідь: 2

Розглянемо розв’язування ірраціональних рівнянь за допомогою заміни змінних.

Якщо до рівняння змінна входить в одному і тому самому вигляді, то зручно відповідний вираз із змінною позначити однією буквою (новою змінною)

Приклад 6. Розв’яжіть рівняння .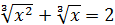

Позначимо 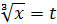. Тоді 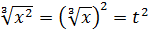. Одержуємо рівняння:

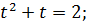
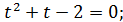
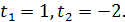
Виконуємо обернену заміну: 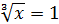, тоді 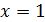або 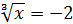−, звідси х = –8.

Відповідь: 1; –8.

Приклад 7. Розв’яжіть рівняння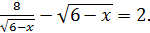

Розв’язання. Нехай 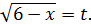Одержуємо

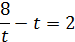
Тоді

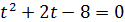
Звідси

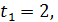
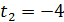
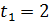— задовольняє умові ;

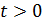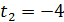— не задовольняє умові .

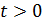Обернена заміна дає:

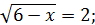
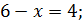
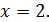
Відповідь: 2.

Приклад 8. Розв’яжіть систему рівнянь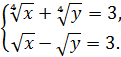

Розв’язання. Заміна 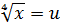і 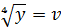дає систему

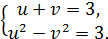
З перøого рівняння цієї системи:

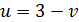
Тоді з другого рівняння одержуємо

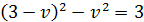
Звідси 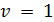, тоді .

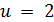Обернена заміна дає:

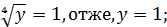
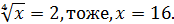
Відповідь: (16;1)

Ми знаємо, що сторонні корені рівняння можна виявити в результаті перевірки.

Коли йдеться про перевірку як про етап розв’язування рівняння, неможливо уникнути проблеми її технічної реалізації. Наприклад, число 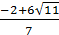є коренем рівняння 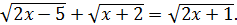Щоб у цьому переконатися треба провести значну обчислювальну роботу.

Для подібних ситуацій можливий інший шлях розв’язування – метод рівносильних перетворень.

Дата добавления: 2015-10-16