Історична довідка

Розділ 1. Теоретичні основі вивчення ірраціональних рівнянь та нерівностей в старшій школі

Історична довідка

Однією із важливих причин появи математичних теорій з'явилося відкриття іррациональності. Термін «раціональне» (число) походить від латиноамериканського слова ratio – відношення, яке є перекладом грецького слова “логос”. На відміну від раціональних чисел, числа, що виражають відношення несумірних величин, були названі ще в старовину ірраціональними, тобто нераціональними (по-грецьки “алогос”). Правда, спочатку терміни “раціональний” і “ірраціональний” відносилися не до чисел, а до сумірних і відповідно не сумірним величинам, які піфагорійці називали вираженими і невираженими, Теодор Киренський же симетричними і асиметричними. У V-VI століттях римські автори Капела і Касіодор перекладали ці терміни на латинь словами rationalis і irrationalis.

Старогрецькі математики класичної епохи користувалися тільки раціональними числами (вірніше цілими, дробами і додатними). У своїх «Початках» Евклід подає вчення про ірраціональності чисто геометрично. Ймовірно, найпершою ірраціональністю, відкритою старогрецькими математиками, було число π. Можна з упевненістю вважати, що початковим пунктом цього відкриття були спроби знайти загальну міру за допомогою алгоритму поперемінного віднімання, відомого зараз як алгоритм Евкліда. Можливо також, що деяку роль зіграло завдання математичної теорії музики: ділення октави, що приводить до пропорції 1:п=п:2. Не останню роль зіграв і характерний для піфагорійської школи загальний інтерес до теоретико-числових проблем.

Багато учених країн Середнього Сходу в своїх працях вживали ірраціональні числа як повноправні об'єкти алгебри. Більш того, коментуючи «Початки» Евкліда і досліджуючи загальну теорію відношення Евдокса, Омар Хайям вже на початку XII ст. теоретично розширює поняття числа до додатного дійсного числа. У тому ж напрямі багато було зроблено найбільшим математиком XIII ст. ат-Туси.

У сучасних навчальних посібниках основа визначення ірраціонального числа спирається на ідеї ал-Каши, Стевіна і Декарта провимірювання відрізків і про необмежене наближення до шуканого числа за допомогою нескінченних десяткових дробів. Проте обгрунтуванням властивостей дійсних чисел і повна теорія їх була розроблена лише в XIXст.

“Джерелом алгебраїчних ірраціональностей є двозначність або багатозначність задачі; бо було б неможливо виразити одним і тим же обчисленням багато значень, що задовольняють одній і тій же задачі, інакше, ніж за допомогою коренів; вони ж хіба лише в окремих випадках можуть бути зведені до раціональностей”. (Лейбніц Г.)

Значення відкриття ірраціональності в математиці важко переоцінити. У математику, мало не вперше, увійшла складна теоретична абстракція, що не має аналога в донауковому загальнолюдському досвіді. Услід за ірраціональністю числа були відкриті багато інших ірраціональності. Так, Теодор Кирени (Vст. до н.е.) встановив ірраціональність квадратного кореня з чисел 3,5,6.,17, які не є повним квадратом, Теетет (410-369 до н.е.) дав одну з перших класифікацій ірраціональностей. З появою ірраціональностей в старогрецькій математиці виникли серйозні труднощі як в теоретико-числовому, так і в геометричному плані.Розв’яжемо задачу: “Віки трьох братів 30, 20 і 6 років. Через скільки років вік старшого дорівнюватиме сумі віків обох молодших братів?”Метод розв’язання подібних задач був відомий ще в II тисячолітті до н.е. писарям Древнього Єгипту (проте вони не застосовували буквеної символіки). Ще складніші завдання уміли розв’язувати з початку II тисячоліття до н.е. в Стародавньому Вавілоні. У математичних текстах, виконаних клинописом на глиняних пластинах, є квадратні і біквадратні рівняння, системи рівнянь з двома невідомими і навіть прості кубічні рівняння. При цьому вавілоняни також не використали букв. На подальший розвиток алгебри сильний вплив зробили розглянуті Діофантом завдання, що приводять до складних систем рівнянь алгебри, зокрема до систем, де число рівнянь було менше числа невідомих. Для таких рівнянь Діофант шукав лише позитивні раціональні розв’язки.З VI ст. центр математичних досліджень переміщається до Індії і Китаю, країн Близького Сходу і Середньої Азії. Китайські учені розробили метод послідовного виключення невідомих для розв’язування систем лінійних рівнянь, подали нові методи наближеного розв’язування рівнянь вищих степенів. Індійські математики використовували від’ємні числа і удосконалили буквену символіку. Проте лише в працях учених Близького Сходу і Середньої Азії алгебра сформувалася в самостійну гілку математики, що трактує питання, пов'язані з розв’язуванням рівнянь. У IX ст. узбецький математик і астроном Мухаммед ал-Хорезми написав трактат “Китаб аль-джебр валь-мукабала”, де дав загальні правила для розв’язування рівнянь першого степеня. Слово «алъ-джебр» (відновлення), від якого нова наука алгебра отримала свою назву, означало перенесення від’ємних членів рівняння з однієї його частини в іншу із зміною знаку. Учені Сходу вивчали і розв’язування кубічних рівнянь, хоча не зуміли отримати загальної формули для їх коренів. У Західній Европі вивчення алгебри почалося в XIII ст. Одним з визначних математиків цього часу був італієць Леонардо Пізанський (Фібоначчі) (бл.1170 – 1228). Його “Книга абака” (1202) – трактат, який містив відомості про арифметику і алгебру до квадратних рівнянь включно. Першим визначним самостійним досягненням західноєвропейських учених було відкриття в XVI ст. формули для розв’язування кубічного рівняння. Це було заслугою італійських алгебраїстів С. Дель Ферро, Н.Тарталья і Дж. Кардано. Учень останнього – Л. Феррарі розв’язав і рівняння 4-го степеня. Вивчення деяких питань, пов'язаних з коренями кубічних рівнянь, привело італійського алгебриста Р. Бомбеллі до відкриття комплексних чисел. Завойовували права громадянства від’ємні числа, потім – комплексні, учені почали вільно застосовувати ірраціональні числа. Особливо далеко було просунуто в XVIII ст. розв’язування систем лінійних рівнянь – для них були отримані формули, що дозволяють виразити розв’язок через коефіцієнти і вільні члени. Подальше вивчення таких систем рівнянь привело до створення теорії матриць і визначників. В кінці XVIII ст. було доведено, що будь-яке рівняння алгебри з комплексними коефіцієнтами має хоч би один комплексний корінь. Це твердження носить назва основної теореми алгебри. Протягом двох з половиною сторіч увага алгебраїстів була прикована до завдання про виведення формули для розв’язування загального рівняння 5-ого степеня. Треба було виразити корені цього рівняння через його коефіцієнти за допомогою арифметичних операцій і витягань коренів (розв’язати рівняння в радикалах). Лише на початку XIX ст. італієць П. Руффіні і норвежець Н. Абель незалежно один від одного довели, що такої формули не існує. Ці дослідження були завершені французьким математиком Е. Галуа, методи якого дозволяють для кожного даного рівняння визначити, чи розв’язується воно в радикалах.На початку XIX ст. були розв’язані основні завдання, що стояли перед алгеброю в першому тисячолітті її розвитку. Були розроблені правила буквеного числення для раціональних і ірраціональних виразів, з'ясовано питання про розв’язування рівнянь в радикалах і побудована строга теорія комплексних чисел. Поверхневому спостерігачеві могло здатися, що тепер математики розв’язуватимуть нові і нові класи рівнянь алгебри, доводитимуть нову тотожність алгебри і так далі. Проте розвиток алгебри пішов іншим шляхом: з науки про буквене числення і рівняння вона перетворилася на загальну науку про операції і їх властивості. Наприклад, ірраціональні рівняння і нерівності можна розглянути як над полем комплексних чисел, так і над полем дійсних чисел.

1.2. Ірраціональні рівняння і нерівності

Рівняння, у яких змінна міститься під знаком кореня, називають ірраціональними.

Найчастіше розв’язування ірраціональних рівнянь ґрунтується на зведені заданого рівняння за допомогою деяких перетворень до раціонального рівняння. Як правило, цього досягають піднесенням обох частин ірраціонального рівняння до одного й того самого степеня, за потреби кілька разів.

Приклад 1. Розглянемо рівняння

Розв’язання. Підносячи обидві частини рівняння отримаємо рівняння, рівносильне даному. Маємо:

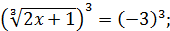
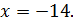
Відповідь: -14

Функція - оборотна, то міркування використані при розв’язування рівняння узагальнимо у теоремі.

Дата добавления: 2015-10-16