Теорема 4. Рівняння виду рівносильне системі

Приклад 10. Розв’яжіть рівняння

Розв’язання. Дане рівняння рівносильне системі

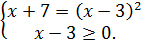
Звідси

Відповідь: .

Теореми 3 та 4 можна узагальнити, керуючись таким очевидним твердженням: якщо і то з рівності випливає, що

Теорема 5. Якщо для будь-якого виконуються нерівності і то рівняння і рівносильні на множині M (Теореми 4 і 5 доводяться відповідно до ідеї доведення Теореми 3).

Приклад 11. Розв’яжіть рівняння

Розв’язання. Вигідно розкласти квадратні тричлени, які стоять під радикалами, на множники:

На цьому етапі є дуже поширена помилка: застосування теореми про корінь з добутку у вигляді Наведений запис формули справедливий лише для і а якщо і , то

Оскільки областю визначення даного рівняння є множина (рис. 1), то дане рівняння рівносильне сукупності двох систем і одного рівняння.

1)

2)

Зрозуміло, що ця система розв’язків не має.

3)

Відповідь: -1; 5.

Стандартний метод розв’язання ірраціональних нерівностей полягає в піднесенні обох частин нерівності в потрібну степінь: якщо нерівність під квадратним коренем, то в квадрат; якщо корінь третьої степені – то в куб і та д. Однак, перетворення нерівності, не порушуючи рівносиль ноті, можливо лише нерівності, у яких обидві частини невід'ємні. При піднесенні до квадрата нерівностей, частини яких мають різні знаки, можуть вийти нерівності, як рівносильні вихідному, так і нерівносильні йому. Простий приклад: -1<3 – нерівність правильне, - теж правильна нерівність. Незважаючи на те, що -4 <-1 - нерівність вірна, нерівність вже не є вірним.

Покажемо, як отримати рівносильні системи для деяких часто зустрічних типів нерівностей.

Нерівність виду

Якщо x лежить в ОДЗ: f (x) ≥ 0, то ліва частина нерівності існує і невід'ємна. Оскільки для всіх x, які є розв'язком даної нерівності, права частина більше лівої, то g (x)> 0. Отже, обидві частини нерівності невід'ємні (для тих x, які є розв'язками нерівності, інші x нас не цікавлять). Значить, зведення в квадрат не порушує равносильности і можна записати рівносильну нашому нерівності систему нерівностей:

Приклад 12. Розв’яжіть нерівність

Відразу перейдемо до рівносильної системи:

Відповідь:

Приклад 13. Розв’яжіть нерівність

Перейдемо до рівносильної системи:

Відповідь:

Нерівність виду

ОДЗ даної нерівності f (x) ≥ 0. Нехай для якихось x з ОДЗ g (x) <0. Тоді, очевидно, всі ці x - розв'язки, так як при цих x ліва частина визначена (x ОДЗ) і невід'ємна, в той час як права частина g (x) <0.

Для інших x з ОДЗ g (x) ≥ 0. Для них обидві частини нерівності невід'ємні, і його можна звести в квадрат: Значить, дане нерівність рівносильна сукупності нерівностей:

Зауважимо, що в останню систему не входить вимога f (x) ≥ 0. Воно й не потрібно, так як виконується автоматично бо повний квадрат завжди невід'ємний.

Приклад 14. Розв’яжемо нерівність

ОДЗ нерівність:

1. Якщо , то всі ці x ОДЗ, для яких вірно x <-1, - розв'язання. Таким чином, - перша частина відповіді.

2. Якщо , то обидві частини нерівності невід'ємні, і його можна звести в квадрат. Маємо:

Отримуємо, що розв’язком є всі .

Об’єднавши результати 1 і 2, отримуємо, .

Відповідь: .

Приклад 15. Розв’яжемо нерівність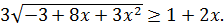

ОДЗ даної нерівності: Будемо розглядати тільки ці x, інші x не можуть бути рішеннями даної нерівності.

1. Якщо , тобто , то всі такі x з ОДЗ, що задовольняють цій умові, є рішеннями нерівності. Значить, все x ≤ -3 - рішення нерівності.

2. Якщо тобто , а з урахуванням ОДЗ це означає, що то обидві частини нерівності невід'ємні. Зведемо обидві частини нерівності в квадрат:

Рівняння має корені:

і . Отже, розв’язком нерівності є . З урахуванням виходить, що на даній множині розв’язком є . Об’єднавши результати 1 і 2, отримуємо,

.

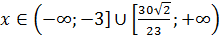Запишемо це розв’язання іншим способом:

Відповідь: .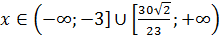

Нерівність виду

ОДЗ даної нерівності: Обидві частини нерівності невід'ємні в ОДЗ, і тому можна зводити в квадрат. Отримаємо рівносильну систему

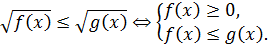
Зауважимо, що з нерівності випливає, що , тобто додатково це вимагати і включати це нерівність в систему не потрібно.

Відзначимо корисне слідство. Припустимо, що ОДЗ нерівності вже знайдено, і ми будемо відбирати розв’язки тільки з ОДЗ (це розумно, оскільки поза ОДЗ розв’язків немає). Тоді вихідна нерівність рівносильне наступному: , а та система, якою це нерівність рівносильно, може бути представлена (для x з ОДЗ) у вигляді 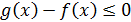. Отже, в ОДЗ

.

Ясно, що ті ж міркування застосовні і для знака нерівності ≥. Звідси можна зробити корисне висновок:

Знак різниці збігається зі знаком вираження

Звідси ж виходить ще одна корисна наслідок:

в ОДЗ:

Приклад 16. Розв’яжемо нерівність

ОДЗ даної нерівності:

Зауважимо, що в ОДЗ x ≥ 0, тому існує і значить

Ми скористалися тут тим, що в ОДЗ x ≥ 0, (x - 5) (x - 6) ≥ 0 і тому існують виписані в останній сходинці корені. Крім того, ми винесли за дужку , який з вищесказаного існує. Цей корінь невід'ємний і тому не впливає на знак нерівності, отже, на нього можна скоротити, не забуваючи, що він може ще перетворитися в нуль і ті x, для яких корінь перетворюється в нуль, є розв'язком нерівності. Таким чином, у відповідь необхідно включити число x = 5. При x = 6 корінь обертається в нуль, але x = 6 не входить в ОДЗ нерівності. Скористаємося тепер тим, що знак різниці коренів збігається зі знаком різниці підкореневих виразів. Маємо:

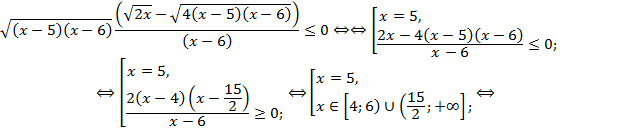
Врахуємо тепер ОДЗ і отримаємо:

Відповідь:

Нерівність виду

ОДЗ даної нерівності: Припустимо, що функції f (x) і g (x) не мають спільних коренів. Розглянемо допоміжну нерівність

1. Якщо g (x) <0, то для будь-якого x з ОДЗ виконано

2. Якщо g (x) ≥ 0, то вираз може мати будь-який знак, але вираз завжди строго додатній. Помноживши обидві частини нерівності на строго додатне число не змінюючи знака нерівності, перейдемо до рівносильної нерівності Таким чином, в ОДЗ

Значить, при , знак різниці збігається зі знаком різниці в ОДЗ.

Отримуємо наступні умови рівносильності.

Запам'ятовувати наведені системи нерівностей не потрібно, важливо розуміти, як вони виходять.

Приклад 17. Розв’яжемо нерівність .

Виконаємо рівносильні в ОДЗ перетворення і наведемо нерівність до зручного для застосування результатів цього пункту увазі.

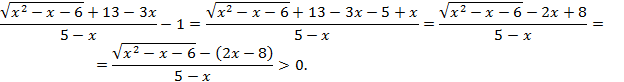
Ми не випадково зробили останнє перетворення. Важливо розуміти, чого тут саме дорівнює функція g (x) = 2 x - 8. Типовою помилкою є вважати, що g (x) = 2 x + 8.

ОДЗ даної нерівності: тобто Тепер перейдемо до рівносильної системи. В ОДЗ

З урахуванням ОДЗ відразу отримуємо:

Відповідь:

1.3. Підходи до вивчення теми «Ірраціональні рівняння і нерівності» в підручниках

Тему «Ірраціональні рівняння і нерівності» не можна віднести до легко засвоюваної. Її традиційне вивчення зосереджене в рамках курсу VIII – ХI класів, що дозволяє повноцінно враховувати вікові можливості учнів у формуванні ряду умінь і навиків, але часу на вивчення теми відведено небагато. Перш за все, відмітимо, що при викладі даної теми реалізуються багато загальних методичних особливостей, характерних для курсу в цілому. У всіх підручниках при вивченні квадратного кореня і його властивостей (8 – 9 класів) розв’язуються прості ірраціональні рівняння виду 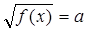де f(x) – многочлен від х, а – деякі числа. Основні ж методи розв’язання ірраціональних рівнянь і нерівностей розглянуті в підручниках 10 – 11 класів (академічного і профільного рівнів).

Проведемо порівняльний аналіз підходів до вивчення ірраціональних рівнянь і нерівностей в різних підручниках «Алгебра і початки аналізу, 10–11».

Підручник А.Н.Колмогорова і ін.(видавництво «Освіта»)— найперший підручник для старшої школи, написаний після реформи 60–70-х років. Це підручник «для всіх», він відрізняється простотою навчальних текстів, має достатню кількість прикладів для розгляду. Але в даному підручнику ще не знайшло віддзеркалення посилення вимог конкурсних іспитів до техніки розв’язування рівнянь, нерівностей, у тому числі і ірраціональних.

Основна змістовна лінія окремих підручників()— дослідження функцій. Ірраціональні рівняння і нерівності вивчаються в 10 класі. У підручниках міститься весь теоретичний і практичний матеріал, необхідний для реалізації навчання на трьох рівнях. Включений різноманітний додатковий матеріал: тести по перевірці готовності вивчення тем, таблиці очікуваних результатів навчання, дослідницькі і лабораторні роботи, довідковий матеріал. Є контрольні завдання трьох рівнів складності, завдання на повторення, історичні відомості і інші матеріали. Але задачного матеріалу явно недостатньо.

В кінці підручника є завдання підвищеної складності, є матеріал для підготовки у вузи. Пропонуються наступні методи розв’язання ірраціональних рівнянь: піднесення обох частин рівняння до п-го степеня; виділення радикала і подвійне піднесення до квадрату; введення нової змінної; метод розв’язання ірраціональних рівнянь, що містять кубічний радикал, а також деякі нестандартні методи. Але підбір рівнянь обмежений, наприклад рівняннями, що мають корені зручні для перевірки. Підручник містить завдання не тільки з простими ірраціональними нерівностями, але і нерівностями,що розв’язуються введенням нової змінної, методом інтервалів. Проте уміння розв’язувати ірраціональні нерівності є необов'язковими для учнів, і відповідний параграф пропонується для самостійного вивчення. Враховуючи сучасні вимоги, що пред'являються на ДПА і на ЗНО для вступу у вищі навчальні заклади до математичної підготовки учнів, і той факт, що дана тема є достатньо важкою для самостійного вивчення учнів, на вивчення розділу повинен знаходитися додатковий час.

При вивченні ірраціональних рівнянь автори обмежуються розглядом розв’язання таких рівнянь, наслідком яких є корені, зручні для перевірки безпосередньою підстановкою в початкове рівняння. І нічого не говорять про складніший випадок, коли така підстановка неможлива, тобто про розв’язанні рівняння переходом до рівняння, рівносильного йому на деякій множині, або переходом до рівносильної системи. При розв’язанні ірраціональних нерівностей автори використовують поняття області визначення нерівності. Є завдання з параметрами. Рівня складності розглянутих в підручнику ірраціональних рівнянь і нерівностей явно недостатньо для розв’язання конкурсних завдань вузів, що пред'являють високі вимоги до математичної підготовки випускників школи. Про це говорить і рівень завдань, які автори включають в контрольні роботи. Тоді не зовсім зрозуміло, чим забезпечується робота класів з поглибленим вивченням математики, якщо автори вважають, що і в них підручник можна використовувати?

Вибираючи підручник для роботи, треба добре знати його особливості, на що він націлений, окрім «виконання програми». У підручнику ключовими положеннями концепції курсу алгебри є:

- математика в школі – не наука, а навчальний предмет;

- математика – предмет швидше |скоріше| гуманітарний, чим природничо-науковий, предмет, основна цінність якого полягає в його загальнокультурній значущості;

стержень курсу – математична мова |язик| і «м'яке» математичне моделювання;

пріоритет в школі віддається функціонально-графічній лінії.

Треба знати «сильні» сторони підручника і способи компенсації його «слабких |слабих|» сторін, не драматизуючи саму наявність недоліків |нестач|. Одна з сильних сторін підручника |посібника| – використання завдань |задавань| розвиваючого характеру.

У старшій школі вивчення математики диференціюється за чотирма програмами: рівень стандарту, академічний, профільний рівень та поглиблене вивчення математики.

Програма рівня стандарту визначає зміст навчання предмета, спрямований на завершення формування в учнів уявлення про математику як елемента загальної культури. При цьому не передбачається, що в подальшому випускники продовжуватимуть вивчати математику або пов’язуватимуть з нею свою професійну діяльність.

Програма академічного рівня задає дещо ширший зміст і вищі вимоги до його засвоєння у порівнянні з рівнем стандарту. Вивчення математики на академічному рівні передбачається передусім у тих випадках, коли вона тісно пов’язана з профільними предметами і забезпечує їх ефективне засвоєння. Крім того, за цією програмою здійснюється математична підготовка старшокласників, які не визначилися щодо напряму спеціалізації.

Програма профільного рівня передбачає вивчення предмета з орієнтацією на майбутню професію, безпосередньо пов’язану з математикою або її застосуванням.

Програма поглибленого вивчення математики розрахована на вивчення математики у 8-11 класах та передбачає поглиблене вивчення предмету.

Таблиця розподілу годин на вивчення математики

за різними рівнями змісту освіти

Навчальні предмети	Кількість годин на тиждень у класах
Рівень стандарту	Академічний рівень	Профільний рівень	Поглиблене вивчення
Математика			-	-	-	-	-	-
Алгебра та початки аналізу	-	-
Геометрія	-	-

У класах фізико-математичного та математичного профілів вивчається два предмети «Алгебра і початки аналізу» та «Геометрія» за програмою профільного рівня.

Учні класів з поглибленим вивченням математики продовжують вивчення двох предметів «Алгебра і початки аналізу» та «Геометрія» за програмою для поглибленого вивчення предмета.

У класах відповідних профілів, замість предмета «Математика» можуть вивчатися окремі курси – «Алгебра та початки аналізу» (із розрахунку 2 години на тиждень в 10 класі і 3 години на тиждень в 11 класі) і «Геометрія» (із розрахунку 2 години на тиждень в 10 класі і 3 години на тиждень в 11 класі) за рахунок часу, відведеного на профільне і поглиблене вивчення предметів, введення курсів за вибором, факультативів.

Зауважимо, що рішення про розподіл годин варіативної складової, відповідно до Положення про загальноосвітній навчальний заклад, приймає навчальний заклад, враховуючи профільне спрямування, регіональні особливості, кадрове забезпечення, матеріально-технічну базу та бажання учнів.

Водночас, учні класів фізичного, економічного та інформаційно-технологічного профілів можуть вивчати предмети «Алгебра і початки аналізу» та «Геометрія» за програмою профільного рівня.

Реалізація профільного навчання математики у 10-11 класах забезпечується системою курсів за вибором (за рахунок варіативного компоненту), які певним чином ураховують інтереси і можливості учнів даного профілю. Курси за вибором поглиблюють та розширюють основний курс математики відповідно до профілю навчання, надають можливості для організації творчої роботи учнів через систему індивідуальних завдань професійної спрямованості.

Дата добавления: 2015-10-16