Теорема 1. Якщо обидві частини ірраціонального рівняння піднести до непарного степеня, то отримаємо рівняння рівносильне даному (на його ОДЗ).

Доведення. Покажемо, що рівняння

(1)

і

(2)

є рівносильними. Нехай число α – корінь рівняння (1). Тоді маємо правильну числову рівність . Звідси можна записати:

Отже, число α є коренем рівняння (2)

Нехай число β – корінь рівняння (2). Тоді отримаємо, що

Оскільки функція , є оборотною, то . Отже, β корінь рівняння (1).

Ми показали, що кожний корінь рівняння (1) е коренем рівнин (2) і навпаки. Це означає, що рівняння (1) і (2) рівносильні.

Приклад 2. Розгляжемо рівняння

Розв’язання. Піднесемо обидві частини рівняння до сьомого степеня. Отримаємо рівносильне рівняння:

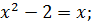
Відповідь: -1;2.

Приклад 3. Розглянемо рівняння (3)

Розв’язання. Природно замінити це рівняння на таке:

(4)

Звідси .

Але перевіривши бачимо, що число не є коренем початкового рівняння. Отже, рівняння (3) не має коренів. Причина появи стороннього кореня полягає в тому, що застосування формули призводить до розширення області визначення рівняння. Тому рівняння (4) є наслідком рівняння (3).

Ще однією причиною появи сторонніх коренів при розв’язуванні ірраціональних рівнянь є необоротність функції Це означає, що з рівності не обов’язково випливає, що . Наприклад, 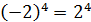, але Водночас із рівності випливає рівність .

Наведені міркування сформулюємо теоремою.

Дата добавления: 2015-10-16