
|
Читайте также: |
Статистическое имитационное моделирование основывается на генерации случайных величин, имитации функционирования системы и статистической обработке результатов моделирования. Методом моделирования может быть исследована СМО любой степени сложности.
Для проведения моделирования могут использоваться как универсальные языки программирования так и проблемно-ориентированные - GPSS, SIMULA и др.
Параметры функционирования системы оцениваются при моделировании по результатам многократного обслуживания требований (многократных испытаний). При имитации работы системы случайные величины (длительность обслуживания в каналах, интервалы между поступлениями требований, время возврата требований в систему, моменты возникновения отказов каналов и их длительность и др.) получают генерацией по ранее приведенным алгоритмам в зависимости от вида распределения (закон, усечение, смещение).
Число обслуживаний (опытов) необходимо принимать таким, чтобы обеспечить оценку интересующих параметров с заданной точностью при принятой доверительной вероятности.
Таким образом, определение числа опытов производится по аналогии с расчетом размера выборки для исследования случайных величин. При этом это число рекомендуется определять в ходе моделирования на основе оценки точности рассчитываемых параметров.
Алгоритмы моделирования ранее рассмотренных систем массового обслуживания приведены на рисунках 2.18 и 2.19. Число моделируемых обслуживаний определяется на основе формулы для нормального закона распределения, а в качестве интересующего показателя принята средняя продолжительность ожидания требованием начала обслуживания. Отноcительная точность оценивания задана равной e с односторонней доверительной вероятностью g= 0.95 (квантиль равна 1.645).
Структура алгоритмов следующая:
блок 2– ввод и вывод на принтер исходных данных;
блоки 3-6 – формирование начальных условий моделирования;
блоки 7-10 – поиск канала (источника) с минимальным значением момента времени освобождения от предыдущего обслуживания (прибытия на обслуживание);
блоки 11-18– имитация обслуживания требований и накопление сумм длительностей времени простоев и обслуживания;
блоки 19-21– принятие решения об окончании моделирования или его продолжении;
блок 22 – наращивание номера опыта (испытания);
блоки 23-24 – вычисление средних значений параметров и вывод их на монитор (принтер).
42.Оценка адекватности уравнения регрессии данным эксперимента
Для проверки существенности коэффициента множественной корреляции и таким образом оценивания согласованности уравнения регрессии с экспериментальными данными используется статистика критерия Фишера
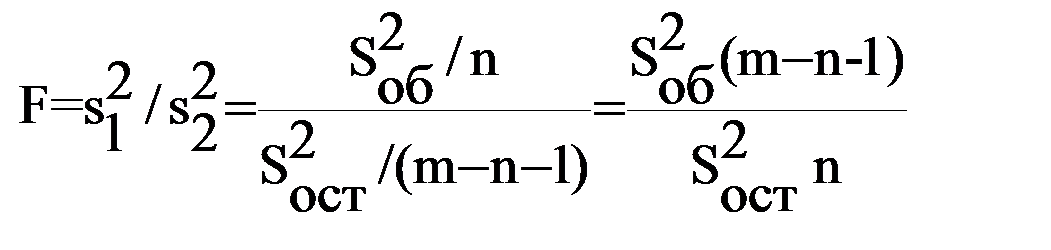 или
или
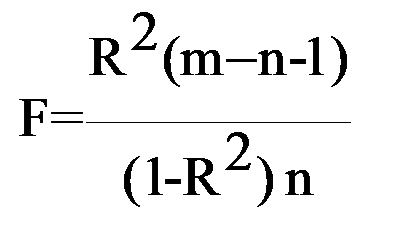 ,
,
где  и
и  – соответственно объясненная и остаточная дисперсия для зависимого параметра.
– соответственно объясненная и остаточная дисперсия для зависимого параметра.
Чтобы не было оснований отвергнуть гипотезу, что экспериментальные данные согласуются с полученным уравнением регрессии, рассчитанная статистика критерия Фишера должна быть больше табличного значения (F > Fт). Табличное значение Fт определяется в зависимости от уровня значимости γ и числа степеней свободы k1 и k2:
k1 = n;
k2= m - n- 1.
Уровень значимости (вероятность) рекомендуется принимать 0.01 – 0.05 (чем меньше, тем жестче требования к адекватности модели).
Если F<Fт, то считается, что уравнение регрессии не согласуется с экспериментальными данными.
43.Оценивание параметров теоретического закона распределения.
Для некоторых законов распределения ниже приведены вид функции плотности вероятности и функции распределения, а также зависимости для вычисления значений параметров.
Дата добавления: 2015-10-16; просмотров: 137 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Критерий Сэвиджа | | | Закон распределения Релея |