Критерий Лапласа

Критерий Лапласа (случай предположения о равновероятных состояниях среды) P(U₁)=P(U₂)=... =P(U_R) имеет решающее правило

.

18.Принятие решений в условиях неопределенностей (критерий Сэвиджа).

При принятии решений в условиях неопределенности информация о состоянии внешней среды (природы) неизвестна принимающему решение (наблюдателю).

Относительно состояния среды наблюдатель может высказывать определенные гипотезы. Такие предположения о вероятном состоянии среды называется субъективными вероятностями P(U_r), r=1,2,...,R. В этом случае имеет место задача принятия решений в условиях риска.

В условиях неопределенности вероятности возможных состояний среды неизвестны. Для выбора оптимальной стратегии в условиях неопределенности Критерий Сэвиджа (критерий минимизации "сожалений") основывается на расчете "сожалений" , равных полезности результата при данном состоянии среды U_r относительно наилучшего решения в зависимости от стратегии X_i как :

.

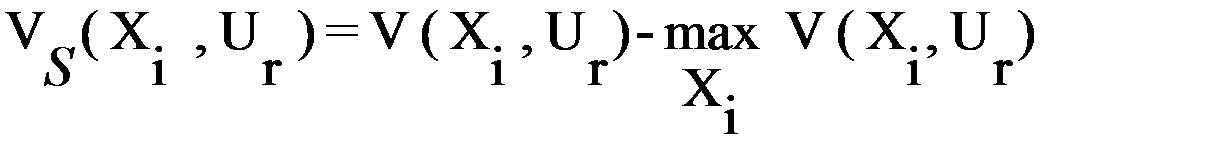К рассчитанным сожалениям применяется решающее правило

.

Этот критерий минимизирует возможные потери при условии, что состояние среды неблагоприятное.

Дата добавления: 2015-10-16