Многоканальная разомкнутая система массового обслуживания

В качестве примера рассматривается многоканальная СМО с простейшим потоком требований и экспоненциальным распределением времени их обслуживания (рисунок 2.16). Система с ожиданием и без приоритетов требований и каналов друг перед другом.

Каналы

Очередь 2

Входящий... Выходящий

поток поток

n

Рисунок 2.16 – Схема многоканальной разомкнутой системы массового обслуживания

Поток требований на обслуживание характеризуется средней интенсивностью L (с^-1, мин^-1, ч^-1, сут^-1) и имеет пуассоновский закон распределения. Доказано, что в этом случае интервалы между поступлениями требований распределены по экспоненциальному закону распределения. Длительность времени обслуживания требования характеризуется средней величиной t_обс (потоком обслуживания v=1/t_обс). Число каналов в системе – n.

Основные показатели функционирования многоканальной разомкнутой системы массового обслуживания рассчитываются по формулам:

вероятность того, что все каналы обслуживания свободны

,

где x = L t_обс – приведенный поток, физическая сущность которого – число каналов, необходимое для обслуживания требований при детерминированных их потоке и времени обслуживания. Должно соблюдаться условие x < n;

вероятность того, что в системе находится ровно k требований

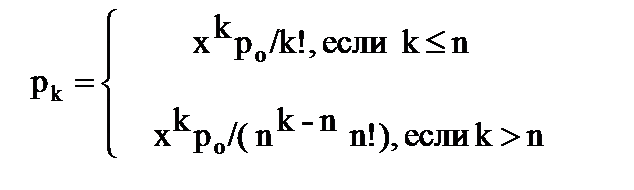
вероятность того, что все каналы заняты

;

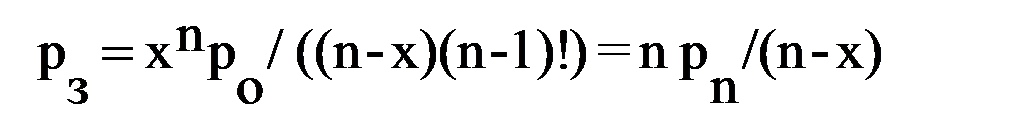вероятность того, что занято ровно n каналов

вероятность того, что время ожидания требованием начала обслуживания t_oж меньше или больше t_з

или

;

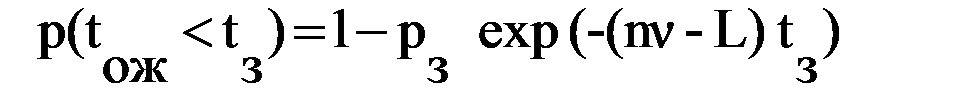среднее число незанятых каналов обслуживания

;

среднее число требований, простаивающих в очереди на обслуживание

;

среднее число требований на обслуживании

;

средняя длительность времени ожидания требованиями начала обслуживания .

Дата добавления: 2015-10-16