Критерий хи - квадрат (Пирсона)

Для его применения вычисляют статистику хи - квадрат по формуле

,

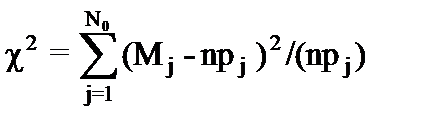где р_j – теоретическая вероятность попадания в j-й интервал случайной величины, которая распределена по выбранному закону распределения с найденными оценками параметров;

np_j – теоретическая частота попадания случайной величины в j-й интервал;

N_о – число интервалов с учетом их объединения для расчета статистики критерия Пирсона.

Для расчета статистики критерия Пирсона интервалы рекомендуется объединять на концах таким образом, чтобы М_j ³5 или np_j ³10. Однако их число N_о должно быть не менее k+2, где k – число параметров рассматриваемой теоретической функции распределения (например, для нормального закона k=2).

Вероятность р_j определяется по формуле

р_j = p(X _j-1 < х < X_j) = F(X _j) - F(X _j-1),

где F(х) – значение функции распределения в точке х.

Значение F(х) определяется по интегральной функции распределения. Для нормального закона распределения значение функции распределения в точке Х_j может быть определено по таблицам или на основе аппроксимации по ранее рассмотренному алгоритму или на основе численного интегрирования. Для логарифмически нормального закона распределения определение теоретических вероятностей производится аналогично как для нормального, но только относительно логарифмов x.

Полученное значение критерия c² необходимо сравнить с табличным c²_g,r для заданного уровня значимости g и числа степеней свободы r. Уровень значимости g представляет собой вероятность отклонения верной гипотезы. Проверку соответствия теоретического и эмпирического распределений рекомендуется проводить при g = 0.05 – 0.1. При больших значениях g выше требования к согласованности распределений.

Число степеней свободы определяется по формуле r = N_о–k–1.

После того, как по таблице квантилей распределения хи-квадрат при заданных g и r найдено c²_g,r , проверяется условие c² <c²_g,r . Если условие выполняется, то гипотеза о распределении случайной величины по рассматриваемому теоретическому закону не отклоняется.

Табличные значения критерия Пирсона приведены ниже:

Дата добавления: 2015-10-16