Уравнение дуги окружности в комплексной форме записи

Рис.1.11 Графическое представление дуги окружности в векторной и комплексной форме

1) Совместим хорду АС с вещественной осью комплексной плоскости: . 2) Обозначим АС через , AD через , DC через , тогда . 3) Здесь вектор опережает вектор на угол ψ.

Предположим, что модуль в -раз больше или меньше модуля , т.е. .

Если:

где . В векторной форме уравнение дуги окружности имеет вид: , откуда

В комплексной форме уравнение дуги окружности можно представить следующим образом

При изменении от 0 до изменяются оба вектора , но таким образом, что угол между ними остается неизменным, при этом сумма тоже остается постоянной равной .

Таким образом: при =var, т.е. 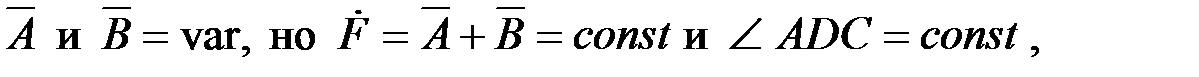при этом конец вектора скользит по дуге окружности , которая опирается на хорду АС, равную . Поэтому можно сказать, что дуга окружности является геометрическим местом точек конца вектора .

Дата добавления: 2015-10-21