Порядок построения круговой векторной диаграммы (КВД) токов

1) Задаем на плоскости положение осей вещественных и мнимых чисел.

2) Выбираем масштаб напряжений для напряжения источника 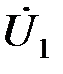и откладываем вектор по оси вещественных чисел. - для идеального источника.

3) Вычисляем ток короткого замыкания: .

Откуда следует, что ток отстает от ЭДС и напряжения источника на угол «».

4) Выбираем масштаб для тока и откладываем вектор под углом «» к вектору ЭДС. Отрезок является хордой круговой диаграммы.

5) Выбираем масштаб сопротивлений и вдоль хорды ОК откладываем отрезок .

6) Из точки А под углом к вектору тока короткого замыкания проводим линию изменяющегося параметра AN.

Примечание: в нашем случае принято, что , тогда . Но так как угол берется со знаком минус (), то получается положительный угол поворота линии переменного параметра AN. А положительный угол в плоскости откладывается против часовой стрелки.

7) Из начала координат отпускаем перпендикуляр OD на линию переменного параметра AN.

8) В середине хорды восстанавливаем второй перпендикуляр до пересечения его с перпендикуляром OD. Точка пересечения двух перпендикуляров дает центр круговой диаграммы – «C».

9) Проводим дугу круговой диаграммы радиусом ОС.

10) На линии переменного параметра AN откладываем отрезок в масштабе сопротивления и соединяем точку с точкой «О» начала координат.

11) Отрезок – текущему значению тока в цепи. При изменении от 0 до 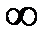точка М (а следовательно конец вектора тока I) перемещается по дуге окружности от точки К к точке «О».

При , ток в электрической цепи пропорционален модулю полной проводимой цепи .

Поэтому отрезок ОМ может служить мерой проводимости цепи в масштабе проводимости. Масштаб проводимости можно найти по режиму короткого замыкания, при котором проводимость всей цепи измеряется отрезком ОК: .

В этом же масштабе можно определить активную «» и реактивную «» проводимости цепи как проекцию отрезка ОМ на ось совпадающую с вектором напряжения и ось мнимых чисел. .

Если , т.е. совпадает с осью вещественных чисел, то комплексы имеют одинаковые аргументы и круговая диаграмма тока, в масштабе проводимости будет являться КВД комплексной проводимости электрической цепи.

Используя КВД можно получить различные величины, характеризующие режим работы электрической цепи.

Рис.1.13 КВД тока для схемы с последовательным соединением комплексных сопротивлений

Из КВД (рис.1.13) имеем:

т.к

Длины отрезков ОК, ОМ и МК пропорциональны напряжениям . Напряжения можно определять соответственно по отрезкам ОМ и МК, пользуясь масштабом напряжения

Направления векторов будут отличаться от направлений векторов ОМ и МК на угол (на КВД они не показаны).

Длина перпендикуляра MF определит активную мощность на входе цепи

.

Отрезок OF на оси мнимых чисел прямой ОР пропорционален реактивной мощности на входе цепи

Полную мощность , активную мощность 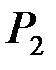и реактивную мощность 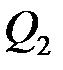нагрузки можно определить из треугольника ОМК с помощью перпендикуляра МН опущенного из точки М на хорду ОК.

Опустим из точки К перпендикуляр на линию и найдем площадь треугольника ОМК

Дата добавления: 2015-10-21