Круговая диаграмма для цепи из двух последовательно соединенных сопротивлений

Рис.1.12 Схема с последовательным соединением комплексных сопротивлений

Для схемы на рис.1.12 заданы комплексные сопротивления:

Известно, что .

Из выражения для аргумента и модуля сопротивления нагрузки следует, что условие возможно тогда, когда убывают или увеличиваются одновременно и пропорционально.

Допустим, что , т.е. характер обоих сопротивлений активно– индуктивный .

В соответствии с законом Ома найдем ток в цепи:

, здесь , т.к. источник ЭДС идеален () и определим геометрическое место точек конца вектора тока при неизменном напряжении на зажимах источника ЭДС (Е). Если принять, что является внутренним сопротивлением источника ЭДС, то в режиме короткого замыкания нагрузки, получим тогда выражение для тока в цепи можно переписать следующим образом:

где , т.к. . Полученное выражение тождественно уравнению . Здесь роль вектора (хорды) играет комплекс тока короткого замыкания .

Роль коэффициента k выполняет отношение сопротивлений Роль вектора (хорды) – вектор (комплекс) играет комплекс текущего значения тока в цепи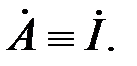

При изменении модуля сопротивления нагрузки вектор текущего значения тока будет скользить по дуге окружности, у которой ток короткого замыкания является хордой.

Дата добавления: 2015-10-21