Графическое изображение зависимостей комплексных величин от параметров

В некоторых случаях вместо зависимости модуля и угла в декартовой системе координат можно построить зависимости от параметра действительной и мнимой части исследуемой комплексной величины. Если изменение модуля сопротивления при постоянном угле φ изображается прямой линией образующей с действительной осью комплексной плоскости угол φ, то изменение угла φ при неизменном модуле сопротивления изображается окружностью с радиусом . Рассмотрим диаграммы сопротивления и проводимости электрической цепи с последовательным, параллельным или смешанным соединением сопротивлений при изменении одного параметра.

1) Последовательное соединение сопротивлений: 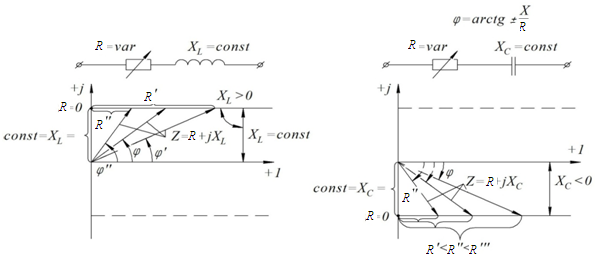а) б)

Рис.1.26 Схемы электрических цепей а, б и их ВД при изменении по величине активного сопротивления

Из анализа ВД на рис.1.26 следует, что при изменении сопротивления “ ” геометрическим местом точек (ГМТ) комплексного сопротивления будет прямая параллельная оси вещественных чисел над или под осью абсцисс, в зависимости от характера реактивного сопротивления.

Геометрическим методом точек комплексной проводимости будет полуокружность, проходящая через начало координат комплексной плоскости , причем диаметр этой полуокружности обратно пропорционален реактивному сопротивлению – .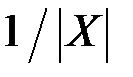

Части полуокружностей, соответствующие отрицательным значениям r, из рассмотрения исключаются.

Значению соответствует наиболее удаленная точка дуги полуокружности, т.к. проводимость возрастает до бесконечности при малом Х.

Значению соответствует точка в начале координат, т.к.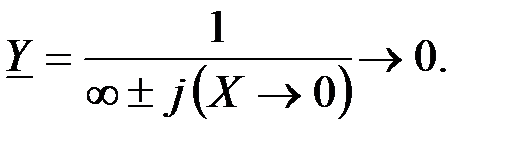

Если активное сопротивление – неизменно (рис.1.27, 1.28), а переменным по величине является реактивное сопротивление, то, как и в первом случае ГМТ комплексного сопротивления будет прямая, но теперь уже параллельная оси мнимых чисел.

ГМТ конца вектора будет окружность, проходящая через начало координат комплексной плоскости, причем диаметр окружности будет равен – активной проводимости.

При цепь имеет только активное сопротивление и соответственно проводимость. При 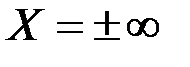проводимость цепи будет равна 0.

Рис.1.27 КВД в случае переменного реактивного сопротивления

а) б) в)

Рис.1.28 Схема с переменным реактивным сопротивлением (а), треугольник сопротивлений (б), когда и КВД (в)

2) Параллельное соединение сопротивлений:

При параллельном соединении элементов (рис.1.29) КВД строится для комплексного сопротивления 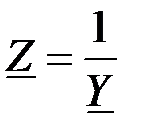. ГМТ для комплексной проводимости будут прямые линии, т.е. линейные ВД.

Дело в том, что при параллельном соединении складываются проводимости, следовательно для схемы приведенной ниже, получим Изобразим ГМТ .

а) б) в)

Рис.1.29 Схема с параллельным соединением элементов (а) когда 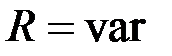, треугольник проводимостей (б) и КВД сопротивлений (в), когда

При изменении реактивного сопротивления (рис.1.30), геометрическое место точек конца вектора комплексной проводимости будет прямая параллельная оси мнимых чисел, а ГМТ конца вектора – полуокружности с диаметром 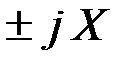проходящие через начало координат.

При полное сопротивление в электрической цепи равно нулю 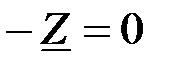. При сопротивление и проводимость цепи являются активными.

а) б) в)

Рис.1.30 Схема с параллельным соединением элементов, (а) когда , треугольник проводимостей (б) и КВД сопротивлений когда

3) Смешанное соединение сопротивлений (рис.1.31):

а) б)

Рис.1.31 – Схема со смешанным соединением элементов (а), когда и КВД сопротивлений, когда

Пусть переменным параметром является реактивное сопротивление: , .

Здесь КВД отличается от предыдущих тем, что окружность смещена относительно начала координат на величину сопротивления . Изменение «» может быть достигнуто изменением частоты или L, C параметров.

1.2 ЭЛЕКТРИЧЕСКИЕ ФИЛЬТРЫ

Электрический фильтр – это ЧП, имеющий резко выраженную избирательную способность для отдельных частот или полос частот.

Полоса частот, в которой затухание мало или отсутствует, называется полосой пропускания или зоной прозрачности. Полоса частот с большим или бесконечно большим затуханием сигнала называется полосой задержания или зоной затухания. Зона прозрачности и зона затухания разделяются частотой среза ()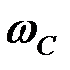

Пассивные электрические фильтры подразделяются:

1) По спектру пропускаемых частот на:

1.1) Фильтры нижних частот (ФНЧ);

1.2) Фильтры высоких частот (ФВЧ);

1.3) Полосовые фильтры (ПФ);

1.4) Заграждающие или режекторные фильтры (ЗФ или РФ),

2) По структуре на симметричные:

2.1) Т – образные;

2.2) П – образные;

2.3.) Мостовые фильтры,

3) По структуре на несимметричные:

3.1 Г – образные,

3.2 Однозвенные и многозвенные,

4) По характеристикам;

4.1) Простые фильтры типа «»;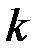

4.2) Производные фильтры типа «m»,

5) В зависимости от элементов схемы фильтра на:

5.1) Реактивные L – C фильтры;

5.2) Резистивные R – C фильтры и др.

Мостовые фильтры содержат большее число элементов, в силу чего имеют большую массу и габариты и в силовых схемах применяются реже.

Наименьшее число элементов, из которых может состоять фильтр равно двум – Г – образный фильтр. «Т» и «П» – образные фильтры могут рассматриваться как комбинация «Г» – образных фильтров [8, 9].

а)

б)  

Рис.1.32 Представление Т (а) и П (б) фильтров в виде Г – образных звеньев

Где сопротивления со стороны параллельной и последовательной ветви.

Параметры последовательного и параллельного звеньев «Т» и «П» – образных фильтров подобраны таким образом, чтобы их меры передачи 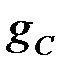были бы численно равны удвоенному значению меры передачи у Г – образного фильтра.

В этом случае обобщенный коэффициент А для «Т» и «П» - образных фильтров как ЧП можно найти как [8, 9]:

(1.39)

Уравнение (1.39) является основным уравнением связи собственных (), обобщенных (A, B, C, D) и характеристических () параметров фильтров как ЧП.

Характеристические сопротивления для «Т» и «П» – образных схем фильтров как ЧП имеют вид [8, 9]:

(1.40)

Для определения границ зоны прозрачности и зоны затухания фильтров используют основное уравнение связи (1.39), которое с учетом может быть преобразовано к виду:

(1.41)

где – коэффициент затухания; 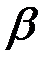– коэффициент фазы.

Так как ЧП обладает свойствами фильтра только в том случае, когда сопротивления имеют разные знаки или разный характер (т.е. L и C):

(1.42)

то для упрощения рассуждений необходимо исключить из правой части уравнения (1.41) единицу:

(1.43)

Тогда уравнение связи параметров преобразуется к виду:

(1.44)

Из (1.44) получаются два условия определяющие зону прозрачности:

1)

2)

Здесь первое условие гласит, что реактивные сопротивления последовательного и параллельного звеньев фильтра должны иметь разные знаки (характер). Если одно из указанных условий нарушается, то это значит, что рассматриваемый диапазон частот принадлежит зоне затухания.

ФИЛЬТРЫ ТИПА «»

Допустим, что составные элементы Г – образного звена являются взаимно обратными двухполюсниками [9]. Это означает, что произведение комплексных сопротивлений последовательного и параллельного звеньев во всем диапазоне частот постоянно:

(1.45)

где k – действительное число.

Если взять произведение [см.(1.40)], то оказывается что оно тоже постоянно:

(1.46)

Поэтому фильтры удовлетворяющие условиям (1.46) и (1.47) получили название фильтров типа «К», схемы которых приведены на рис.1.33 ÷ 1.36.

Рис.1.33 Фильтр нижних частот типа «»

Рис.1.34 Фильтр верхних частот типа «»

Рис.1.35 Полосовой фильтр типа «»

Рис.1.36 Заграждающий фильтр типа «»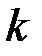

Физические свойства фильтров объясняются тем, что на низких частотах (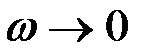) индуктивные сопротивления малы (), а емкостные сопротивления () велики; на высоких же частотах имеет место обратное явление – индуктивные сопротивления велики, а емкостные малы. Поэтому например, в фильтре, нижних частот (см.рис.1.33) токи нижних частот проходят через индуктивность в нагрузку, лишь в малой степени ответвляясь в емкость. В области же верхних частот индуктивность представляет большое сопротивление и, кроме того, ток высокой частоты, прошедший через индуктивность, замыкается в основном через емкость, имеющую для него малое сопротивление.

Аналогичные рассуждения применимы и к фильтрам верхних частот (см.рис.1.34), которые благодаря емкостному характеру сопротивления продольной ветви и индуктивному характеру сопротивления поперечной ветви обусловливаются большое затухание на нижних частотах и малое затухание на верхних.

В свою очередь в полосовых и заграждающих фильтрах (рис.1.35 и 1.36) проявляются частотные зависимости сопротивлений двухполюсников, состоящих из последовательно и параллельно соединенных индуктивностей и емкостей.

Частотные характеристики 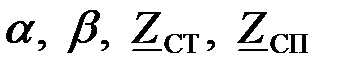рассматриваемых фильтров типа «» изображены на рис. 1.37 – 1.40, а расчетные выражения основных характеристик и параметров фильтров сведены в табл. 1 и 2.

Как видно из расчетных выражений и характеристики, в пределах полосы пропускания напряжение на входе симметричного фильтра, нагруженного согласованно, опережает напряжение на выходе ( – фильтр нижних частот) или отстает от него ( – у фильтров верхних частот).

В случае полосового фильтра (рис.1.39) знак изменяется в пределах полосы пропускания с минуса на плюс. У заграждающего фильтра знак меняется с плюса на минус в полосе затухания (рис.1.40).

В полосе задерживания симметричного фильтра коэффициент фазы равен (+π) (фильтр нижних частот) или (– π) (фильтр верхних частот); в случае симметричного полосового фильтра коэффициент фазы ниже полосы пропускания равен (– π), а выше полосы пропускания – равен (+π). У заграждающего фильтра коэффициент фазы в диапазоне от частоты среза до частоты всплеска затухания 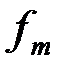положительный (+π), а от частоты всплеска затухания до частоты среза 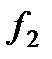, β имеет отрицательный знак (-π) (рис.1.40).

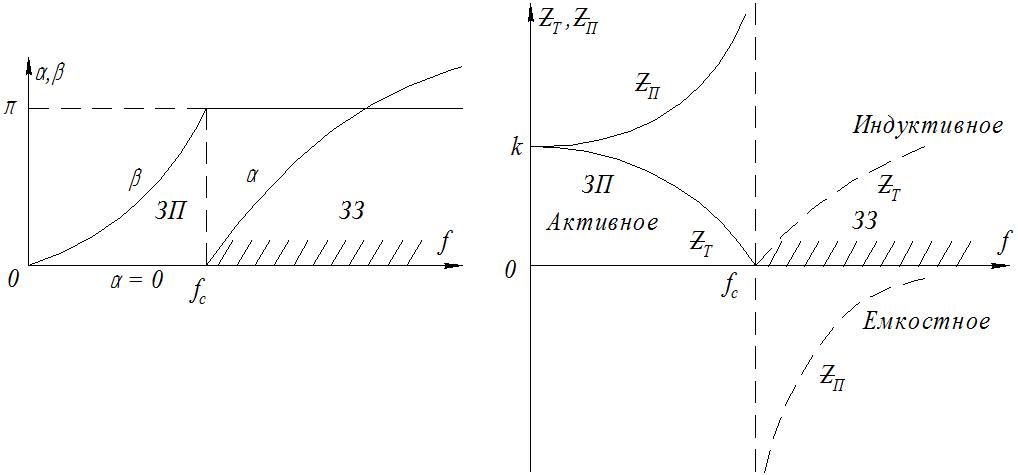
Рис.1.37 Частотные характеристики фильтра нижних частот типа «»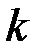

Рис.1.38 Частотные характеристики фильтра верхних частот типа «»

Рис.1.39 Частотные характеристики полосового фильтра типа «»

Рис.1.40 Частотные характеристики заграждающего фильтра типа «»

Таблица 1 Основные характеристики фильтров

Характеристики	Фильтр нижних частот	Фильтр верхних частот	Полосовой фильтр	Заграждающий фильтр
Полоса пропускания
Полоса задерживания

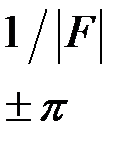
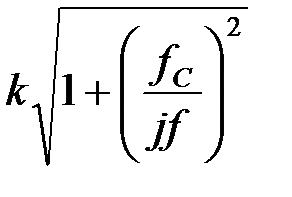
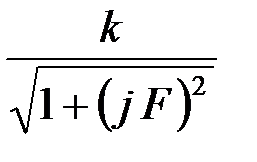
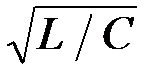
Таблица 2 Расчетные параметры фильтра

Фильтр нижних частот	Фильтр верхних частот	Полосовой фильтр	Заграждающий фильтр

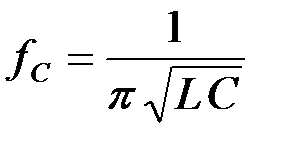
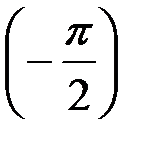Выше отмечалось, что коэффициент фазы Г-образного фильтра равен , и поэтому в полосе задерживания он равен или в зависимости от типа фильтра.

Если Г – образный фильтр нагружен согласованно, то угол фазового сдвига между напряжениями на входе и выходе составляет , где и – углы характеристических сопротивлений рассматриваемого Г – образного фильтра [8].

В полосе затухания характеристические сопротивления мнимые, разного знака и соответственно разность углов составляет 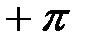или . В этом случае угол между входным и выходным напряжениями Г-образного фильтра, нагруженного согласованно, с учетом того, что в полосе затухания , получается равным . Это соответствует физическим представлениям о фазовых сдвигах в реактивных цепях, поскольку в полосе затухания нагрузка предполагается также реактивной.

Следует заметить, что если, например, Г – образный фильтр нижних частот согласованно нагружен со стороны выхода, имеющего характеристическое сопротивление , то в полосе пропускания нагрузка фильтра, равная 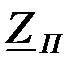, будет иметь активный характер.

Можно показать, что в результате параллельного соединения активного сопротивления нагрузки с емкостным сопротивлением поперечной ветви Г – образного звена получится активно-емкостное сопротивление, емкостная составляющая которого компенсирует индуктивное сопротивление продольной ветви . В результате останется только активная составляющая, равная характеристическому сопротивлению при данной частоте .

Для определения знака характеристического сопротивления фильтра в полосе затухания (+ j или - j) удобно пользоваться значения и в табл.1, в которых под корнем сохранен множитель j. В полосе задерживания слагаемое, содержащее множитель j больше единицы; поэтому при отбрасывании «1» под корнем остается выражение с множителем j в числителе или знаменателе в зависимости от типа фильтра и от того, рассматривается 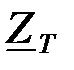ли или .

Преимуществом фильтров типа «» является их простота, а также то, что в полосе затухания по мере удаления частоты от частоты среза неуклонно возрастает.

Что касается недостатков фильтров типа «», то они в основном заключаются в следующем:

1) Характеристические сопротивления 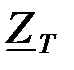и 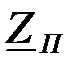в полосе пропускания фильтра резко изменяются в зависимости от частоты, вследствие чего согласовать нагрузку с фильтром удается только на одной строго фиксированной частоте.

2) Кривая затухания вблизи частоты среза имеет недостаточную крутизну, вследствие чего не обеспечивается четкое разделение полосы пропускания и зоны затухания.

Для увеличения крутизны кривой затухания приходится применять многозвенные или производные фильтры.

ПРОИЗВОДНЫЕ ФИЛЬТРЫ ТИПА «»

В целях наилучшего согласования нагрузки с фильтром необходимо, чтобы характеристическое сопротивление фильтра было по возможности постоянным в полосе пропускаемых частот. В связи с этим необходимо изменить сопротивление продольной или поперечной ветвей Г – образного звена типа «» таким образом, чтобы получилось новое Г-образное звено с характеристическим сопротивлением, мало меняющимся в зависимости от частоты в полосе пропускания. Второе характеристическое сопротивление этого звена должно быть равно характеристическому сопротивлению исходного звена типа «» (именуемого «прототипом»).

Равенство характеристических сопротивлений производного фильтра (так называемого фильтра типа «m»)и фильтра прототипа (фильтра типа «») позволяет включать их согласованно и образовывать, таким образом, комбинированные фильтры, сочетающие в себе преимущества фильтров обоих типов. Ввиду того, что Г – образный прототип имеет два сопротивления, то в общем случае возможны два варианта:

1) Одинаковыми остаются характеристические сопротивления (рис.1.41). Полученное при этом звено «m» носит название последовательно-производного.

2) Одинаковыми остаются характеристические сопротивления (рис.1.42). В этом случае звено «m» носит название параллельно-производного.

а) б)

Рис.1.41 Образование последовательно-производного звена типа «m»

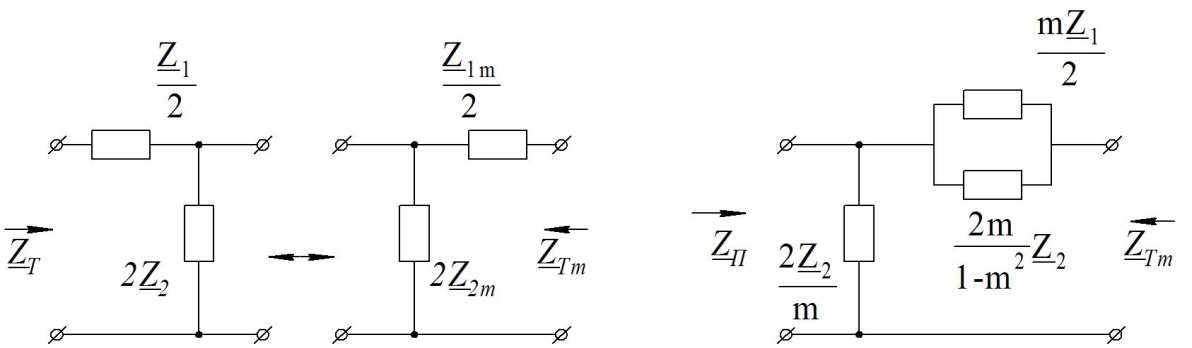
а) б)

Рис.1.42 Образование параллельно-производного звена типа «m»

Рассмотрим первый вариант. Из условия равенства характеристических сопротивлений 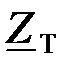звеньев, изображенных на рис. 1.41, а и б, следует:

(1.48)

Пусть 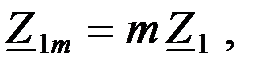(1.49)

причем (1.50) Подстановка (1.49) в (1.48) и решение полученного уравнения относительно 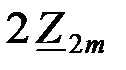дают:

(1.51)

Из этого выражения видно, что поперечное плечо последовательно-произвольного Г – образного звена типа «m» состоит из двух последовательно включенных сопротивлени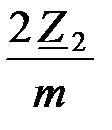й:

и (см.рис.1.41, б).

Рассмотрим вариант определениея параллельно-производного звена типа «m». Исходя из условия равенства характеристических сопротивлений применительно к рис.1.42, а и б, имеем равенство характеристических сопротивлений прототипа и производного фильтра:

Пусть 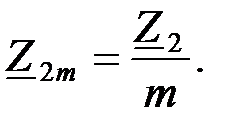(1.53)

После подстановки (1.53) в (1.52) решение уравнения относительно дает: (1.54)

Значит, продольное плечо параллельно-производного Г-образного звена типа «m» состоит из двух сопротивлений и , соединенных параллельно (рис.1.42, б).

В соответствии с (1.51) и (1.54) могут быть найдены выражения характеристических сопротивлений 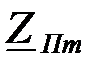(рис.1.41) и 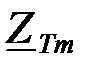(рис.1.42):

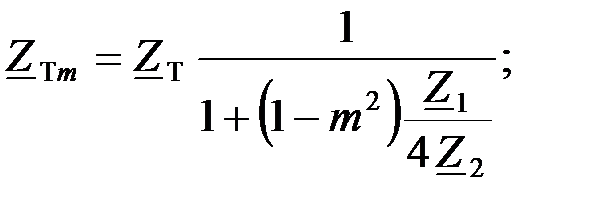(1.55)

(1.56)

Очевидным является соотношение

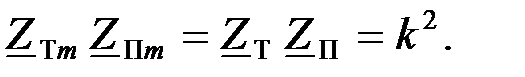(1.57)

Полосы пропускания фильтров типа «» и полученных из них производных фильтров типа «m» совпадают. Действительно, взяв отношение (1.49) к (1.51) получим:

; (1.58)

аналогичное выражение получается на основании (1.53) и (1.54) для другого варианта фильтра типа «m».

Подставляя в (1.58) условия и , отвечающие предельным частотам фильтра типа «», получаем:

(1.59)

Условия (1.59) соответствуют предельным частотам производного фильтра типа «m» (имеющего последовательно- или параллельно-производное звено).

Следовательно, частоты среза для обоих типов фильтров совпадают.

О совпадении полос пропускания фильтра-прототипа и производного фильтра можно также судить на основании равенства характеристических сопротивлений (в полосе пропускания характеристические сопротивления имеют действительные значения).

В полосе задерживания затухание определяется как [9]:

. (1.60)

Из (1.60) следует, что затухание обращается в бесконечность при частоте , при которой , или, что то же когда При этих условиях , выражаемое формулой (1.51), обращается в нуль. Это означает, что при наступает резонанс напряжений в поперечной ветви (в случае последовательно-производного звена). При этих же условиях , выражаемое формулой (1.59), обращается в бесконечность, что означает резонанс токов в продольной ветви (в случае параллельно-производного звена).

Частота называется частотой бесконечно большого затухания или частотой всплеска затухания.

При переходе частоты через значение , т.е. в области частот (когда ) или (когда ), сопротивления обоих плеч фильтра и имеют одинаковый знак. В этом случае в соответствии с левой частью формулы (1.60) гиперболический косинус должен быть заменен гиперболическим синусом.

При , стремящемся к нулю,

(1.61)

На рис.1.43 показано семейство кривых собственного затухания α фильтра типа «m» (при разных значениях «m») в функции . При m = 1 кривая затухания обращается в характеристику фильтра типа «». Чем меньше коэффициент «m», тем меньше значение , т.е. тем круче кривая коэффициента затухания α. Однако, как видно из рис. 1.43, предельное значение «α» при уменьшается по мере снижения «m».

Рис.1.43 Кривые затухания фильтра типа «m»

На рис.1.44 изображены кривые или в зависимости от величины , равной для фильтров нижних частот и для фильтров верхних частот.

В спектре частот, соответствующем 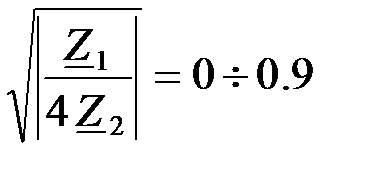, характеристические сопротивления и отклоняются от на при m = 0.54.

Рис.1.44 Характеристическое сопротивление фильтра типа «m»

Типовые схемы Г – образных фильтров нижних частот, верхних частот и полосовых фильтров типов «» и «m» приведены на риc. 1.45 – 1.47; частотные характеристики фильтров типа «m» представлены на рис. 1.48 – 1.50.

Рис.1.45 Фильтр нижних частот типа «m»

Рис.1.46 Фильтр верхних частот типа «m»

Рис.1.47 Полосовой фильтр типа «m»

Рис.1.48 Частотные характеристики фильтра нижних частот типа «m»

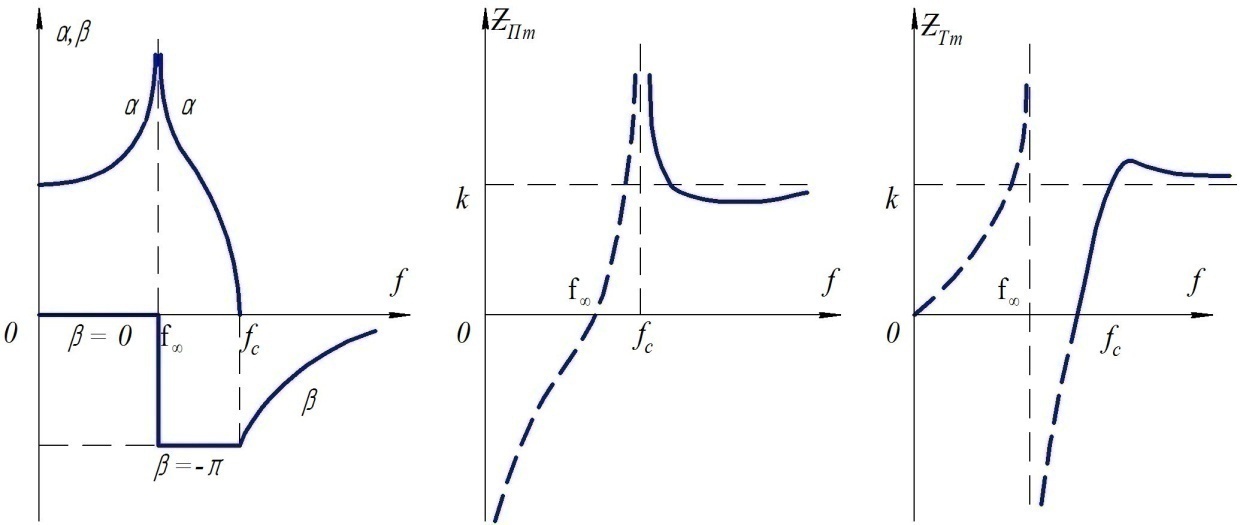
Рис.1.49 Частотные характеристики фильтра верхних частот типа «m»

Рис.1.50 Частотные характеристики полосового фильтра типа «m»

Как видно из частотных характеристик, фильтры типа «m» имеют более постоянное характеристическое сопротивление в полосе пропускания, чем фильтры типа «». Кроме того, они обладают большей крутизной кривой коэффициента затухания.

Соединяя последовательно звенья фильтров типов «» и «m», можно достигнуть некоторого постоянства характеристических сопротивлений и высокой крутизны кривой коэффициента затухания при одновременном сохранении необходимо затухания ниже или выше частоты бесконечно большого затухания. На рис.1.50.а в виде примера показан полосовой фильтр, состоящий из Т-образного фильтра типа «» (в середине) и двух Г – образных звеньев типа «m» (по концам). На рис.1.50.б изображена частотная характеристика коэффициента затухания комбинированного фильтра.

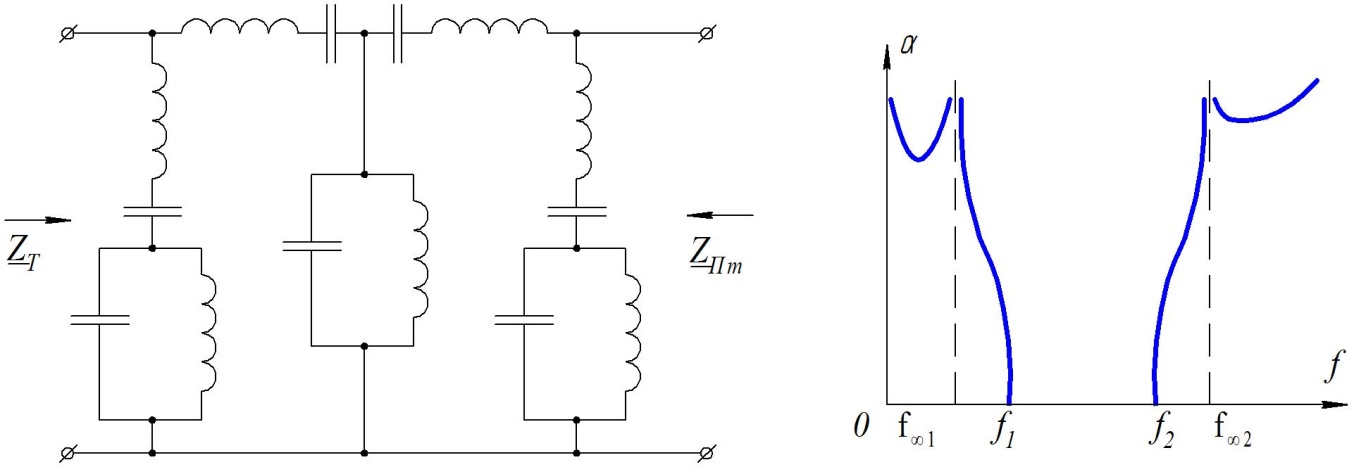
Рис.1.50 Комбинированный фильтр

Дата добавления: 2015-10-21