Круговая диаграмма для любой развлетвленной цепи

Круговую диаграмму можно построить для любой разветвленной электрической цепи, если в ней изменяется только одно сопротивление (рис.1.23).

Рис.1.23 Схема с активным четырехполюсником

Такую электрическую цепь всегда можно представить в виде четырехполюсника (ЧП). Если все элементы электрической цепи ЧП линейны, то токи на входе и выходе ЧП будут связаны линейными соотношениями:

Рассмотрим уравнение , вначале, в режиме ХХ (рис.1.23). 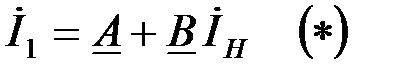, где «А» и «В» – комплексные числа. Пусть модуль сопротивления нагрузки – изменяется таким образом, чтобы . Тогда, рассматривая ЧП вместе с первичным контуром относительно зажимов сопротивления (рис.1.24) как активный двухполюсник (источник энергии с некоторым внутренним сопротивлением), – несложно показать, что конец вектора тока при изменении будет описывать дугу окружности.

Чтобы определить комплексы «А» и «В» связывающие , нужно знать значения токов для каких-нибудь двух крайних режимов: например, при

Рис.1.24 Схема замещения активного четырехполюсника

Рассмотрим уравнение , вначале в режиме холостого хода (рис.1.23).

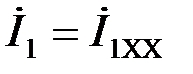1) При (обрыв) , пусть при этом . Тогда из уравнения получаем: .

2) При (короткое замыкание) , пусть при этом . Тогда из уравнения получим: или , откуда , тогда уравнения может быть преобразовано к виду: .

На основании закона Ома для схемы двухполюсника (рис.1.24) получим:

где входное сопротивление всей цепи со стороны относительно зажимов сопротивления нагрузки.

Тогда по теореме об активном двухполюснике [1]:

, где .

С учетом последнего соотношения уравнение круговой диаграммы преобразуется к виду:

,

Уравнение может быть представлено круговой диаграммой с хордой . Для построения КВД необходимо предварительно определить и (со стороны зажимов pq).

Порядок построения КВД ЧП:

1) Выбираем масштаб напряжения и откладываем вдоль непроявленной оси ординат .

2) Выбираем масштаб тока и откладываем и . Предположим при этом, что , а .

3) Соединяя концы векторов и , получаем хорду .

4) Выбирая масштаб , откладывали на хорде - отрезок .

5) Проводим прямую изменяющегося параметра под углом .

6) Опускаем перпендикуляр на из точки и восстанавливаем перпендикуляр из середины . Тогда точка пересечения двух перпендикуляров является центром круговой диаграммы “C”. Радиусом проводим дугу окружности.

7) На линии переменного параметра откладываем сопротивление нагрузки и соединяем конец AN с точкой .

8) Точка пересечения линии с дугой окружности точки М при изменении сопротивления нагрузки перемещается по дуге Отрезок в масштабе тока дает ток в нагрузке , отрезок ОМ дает ток на входе ЧП. Отрезок МК в масштабе напряжения определяет напряжение в нагрузке.

9) Используя КВД можно определять и энергетические характеристики ЧП:

Рис.1.25 КВД токов и напряжений схемы с активным четырехполюсником активным четырехполюсником

Дата добавления: 2015-10-21