Перечень условных обозначений

– мгновенное значение переменной электродвижущей силы (ЭДС), В;

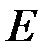– действующее значение переменной электродвижущей силы (ЭДС), В;

– амплитудное значение переменной электродвижущей силы (ЭДС), В;

– комплексное изображение переменной синусоидальной электродвижущей силы (ЭДС), В;

– мгновенное значение переменного напряжения, В;

– действующее значение переменного напряжения, В;

– амплитудное значение переменного напряжения, В;

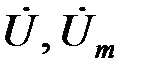– комплексное изображение переменного синусоидального напряжения, В;

– мгновенное значение переменного тока, А;

– действующее значение переменного тока, А;

– амплитудное значение переменного тока, А;

– комплексное изображение переменного синусоидального тока, А;

– мгновенное значение переменного тока источника тока, А;

– действующее значение переменного тока источника тока, А;

– комплексное изображение переменного синусоидального тока источника тока, А;

– начальная фаза (начальный фазовый сдвиг);

– угол сдвига по фазе;

– мнимая единица;

Re – значение действительной части комплексного числа;

Im – значение мнимой части комплексного числа;

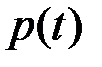– мгновенная мощность, Вт;

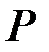– активная мощность, Вт;

– реактивная мощность, ВАр;

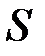– полная мощность, ВА;

– комплексное изображение полной мощности, ВА;

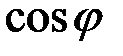– коэффициент мощности;

– период переменного тока, с;

– частота переменного тока, Гц;

– угловая частота переменного тока, рад/с;

– омическое сопротивление резистора, Ом;

– омическая проводимость ветви, 1/Ом или См (Сименс);

– индуктивность катушки, Гн;

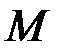– взаимная индуктивность катушки, Гн;

– индуктивное сопротивление катушки, Ом;

– взаимоиндуктивное сопротивление, Ом;

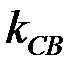– коэффициент магнитной связи;

– емкость конденсатора, Ф;

– емкостное сопротивление конденсатора, Ом;

– модуль полного сопротивления, Ом;

– полное комплексное сопротивление, Ом;

– характеристическое сопротивление, Ом;

– реактивное сопротивление, Ом;

– модуль полной проводимости, См (Сименс);

– полная комплексная проводимости, См (Сименс);

– реактивная проводимость, См;

– потокосцепление, Вб;

– магнитный поток, Вб;

– резонансная частота переменного тока, Гц;

– резонансная угловая частота переменного тока, рад/с;

– мера передачи;

– коэффициент затухания;

– коэффициент фазы;

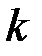– номинальное волновое сопротивление, Ом;

– коэффициент передачи;

– передаточная функция;

ЧП – четырехполюсник;

ВД – векторная диаграмма;

КВД – круговая векторная диаграмма;

ФНЧ – фильтр низкой частоты;

ФВЧ – фильтр высокой частоты;

ПФ – полосовой фильтр;

ЗФ – заграждающий фильтр.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ

1.1 ЧЕТЫРЕХПОЛЮСНИКИ И КРУГОВЫЕ ДИАГРАММЫ

Четырехполюсником (ЧП) называется электрическая схема («черный ящик»), имеющий два входных и два выходных зажима.

ЧП принято изображать в виде прямоугольника. Если ЧП содержит источник энергии, то на поле прямоугольника ставят печатную букву «А» (активный). Если буква «А» отсутствует, значит, ЧП пассивный, т.е. составлен из R - L - C элементов. Примеры активных ЧП – источники электропитания, усилители мощности, активные фильтры. Примеры пассивных ЧП – трансформаторы, пассивные электрические R - C и L - C фильтры, электрические цепи с распределенными параметрами (длинные линии).

В общем случае ЧП характеризуется двумя входными параметрами (рис.1.1) – током и напряжением и двумя выходными параметрами – током и напряжением .

Рис.1.1. Обобщенная схема ЧП для «А» формы записи уравнений

В зависимости от состава элементов ЧП, схемы соединения элементов (Т, П, Г – образные) и свойств элементов ЧП подразделяются на:

1) Активные и пассивные;

2) Линейные и нелинейные;

3) Симметричные и несимметричные;

4) Уравновешенные и неуравновешенные;

5) Лестничные и мостовые.

Так как ЧП в общем случае характеризуется четырьмя параметрами – двумя напряжениями и и двумя токами и , то по крайней мере два из них можно выразить через два других, например, представить в виде зависимостей

или, наоборот

Число сочетаний из четырех элементов по два можно найти, как число сочетаний из четырех элементов по два:

следовательно, в самом общем случае можно получить шесть форм записи уравнений связи входных и выходных параметров ЧП.

Уравнения ЧП в «А» и «B» формах записи имеют вид [1]:

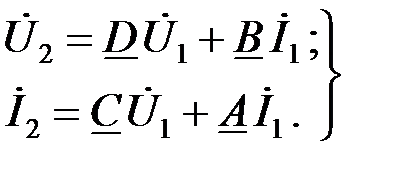«А» «B» (1.1)

Уравнения ЧП в «Z» и «Y» формах записи:

«Z» «Y» (1.2)

Уравнения ЧП в «H» и «G» формах записи:

«H» «G» (1.3)

Между «А» и «B», «Z» и «Y», «H» и «G» формами записи уравнений имеет место попарная инверсия.

Уравнения ЧП в «B» форме записи получены для схемы ЧП представленной на рис.1.2.а, уравнения в «Z» и «Y», «H» и «G» формах записи – для схемы ЧП, представленной на рис.1.2.б:

а) б)

Рис.1.2 Обобщенные схемы ЧП для «B» (а), «Z» и «Y», «H» и «G» формах записи уравнений

Коэффициенты всех форм записи уравнений ЧП могут быть найдены как теоретически, так и опытным путем. Исторически сложилось так, что «А» форма в электротехнике считается основной.

Коэффициенты A, B, C, D ЧП в «А» форме записи являются постоянными комплексными величинами, зависящими от активных и реактивных сопротивлений элементов схемы и от способа их соединения. Связь между обобщенными коэффициентами у взаимных ЧП имеет вид [1, 2 ]: AD – BC = 1.

Для симметричного ЧП A = D (симметричность определяется равенством его сопротивлений со стороны входных и выходных зажимов). ЧП со сложной схемой можно заменить более простым, ему эквивалентным, если известны A, B, C, D коэффициенты. Наиболее простыми схемами замещения ЧП является Т – образная и П – образная схемы (рис.1.3).

Рис.1.3 Схема замещения четырехполюсника

Сопротивления 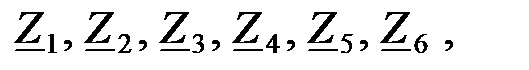отображающие внутреннюю структуру ЧП называются собственными параметрами ЧП.

A, B, C, D коэффициенты ЧП можно вычислить через собственные сопротивления Т-образной и П-образной схем замещения (рис.1.3) [1, 2]:

–

в случае Т – схемы замещения;

–

в случае П – схемы замещения.

В свою очередь собственные сопротивления схемы замещения можно определить через A, B, C, D коэффициенты ЧП:

Наиболее просто значения A, B, C, D коэффициентов ЧП определяются из опытов холостого хода и короткого замыкания.

Рассмотрим питание ЧП со стороны зажимов «mn» при холостом ходе (ХХ) (обрыве) зажимов «pq» (рис.1.1). В этом случае (см. рис.1.4),

Рис.1.4 Холостой ход зажимов «pq»

Тогда уравнения ЧП (1.1) в «A» форме записи в режиме ХХ зажимов «pq» будут иметь вид:

откуда (1.4)

Входное сопротивление ЧП со стороны зажимов “mn” при разомкнутых зажимах “pq” с учетом (1.4.):

(1.5)

При питании ЧП со стороны зажимов «mn» и коротком замыкании вторичных зажимов «pq», схему на рис.1.1 можно привести к виду на рис.1.5. В этом случае

(см. рис.1.5),

Рис.1.5 Короткое замыкание зажимов «pq»

Тогда уравнения ЧП (1.1) в «A» форме записи в режиме КЗ зажимов «pq» будут иметь вид:

откуда (1.6)

Входное сопротивление ЧП со стороны зажимов “mn” при коротком замыкании зажимов «pq» с учетом (1.6.) найдем как

(1.7)

Так как в общем случае ЧП может иметь несимметричную внутреннюю структуру, то необходимо повторить опыты холостого хода (ХХ) и короткого замыкания (КЗ), но для случая перемены зажимов подключения источника питания и нагрузки.

Пусть питание ЧП осуществляется со стороны зажимов «pq», при холостом ходе (обрыве) ветви «mn» (рис.1.2.а). В этом случае, а схема ЧП представлена на рис.1.6.

Рис.1.6 Холостой ход зажимов «mn»

Тогда, уравнения ЧП (1.1) в «B» форме записи в режиме ХХ зажимов «mn» (рис.1.2.а) будут иметь вид:

тогда (1.8)

Входное сопротивление ЧП со стороны вторичных зажимов «pq» при холостом ходе ветви «mn» найдем как:

(1.9)

При питании ЧП со стороны зажимов «pq» и коротком замыкании зажимов «mn», тогда схему на рис.1.2.а, можно привести к виду на рис.1.7:

Рис.1.7 Короткое замыкание зажимов «mn»

Уравнения ЧП (1.1) в «B» форме записи в режиме замыкания зажимов «mn» (см. рис.1.7) будут иметь вид:

откуда (1.10)

Входное сопротивление ЧП со стороны зажимов «pq» при коротком замыкании зажимов «mn» найдем как:

(1.11)

Решая совместно уравнения (1.5), (1.9), (1.11) с уравнением связи A, B, C, D коэффициентов ЧП (1.4), получим:

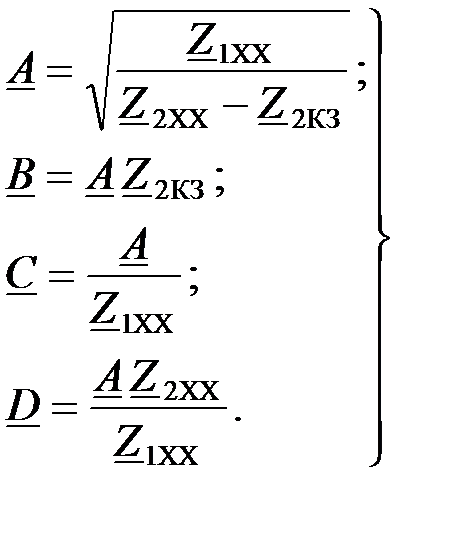(1.12)

Используя полученные выше уравнения (1.4), (1.6), (1.8), (1.10) можно выразить выходное напряжение и выходной ток через отношения входных напряжений и и токов и к соответствующим A, B, C, D коэффициентам ЧП:

или (1.13)

Подставляя соотношения из (1.13) в уравнения ЧП, например в «А» форме записи (1.1), получим:

(1.14)

Из (1.14) следует, что напряжение и ток ЧП при нагрузке могут быть выражены геометрической суммой напряжений и токов в режимах холостого хода и короткого замыкания ЧП.

Связь между сопротивлениями ХХ и КЗ имеет вид:

(1.15)

Входное сопротивление ЧП со стороны зажимов «mn» под нагрузкой можно найти, воспользовавшись уравнениями ЧП в «А» форме записи (1.1):

(1.16)

Аналогично, используя уравнения ЧП в «B» форме записи (1.1) входное сопротивление ЧП со стороны зажимов “pq” под нагрузкой найдем как:

(1.17)

Из (1.16) и (1.17) следует, что несимметричные ЧП могут использоваться для преобразования сопротивлений нагрузки, т.е. как трансформаторы сопротивлений.

Дата добавления: 2015-10-21