
Читайте также:
|
Схема пассивного двухполюсника с двумя параллельными ветвями представлена на рис.1.15.
Построим круговую диаграмму для R-C ветви, пологая, что кроме емкости С все остальные параметры схемы постоянны.

|
1) Найдем комплекс входного тока электрической цепи
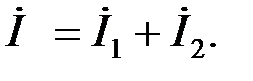 Уподобим заданную электрическую цепь ранее рассмотренной (см. рис.1.16).
Уподобим заданную электрическую цепь ранее рассмотренной (см. рис.1.16).
 Рис.1.16 Эквивалентная схема замещения параллельной схемы
Рис.1.16 Эквивалентная схема замещения параллельной схемы
| 2) Ток в первой R-L ветви на рис.1.15 будет неизменным: 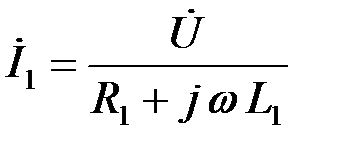 , т.к. , т.к. 
|
3) Ток во второй R-C ветви:  – зависит от емкости С, и должен изменяться по круговой диаграмме:
– зависит от емкости С, и должен изменяться по круговой диаграмме: 
Т.к. «R-C» и «R-L» ветви включены параллельно, то можно процессы в них рассматривать отдельно, при включении каждой ветви на источник энергии в точках a и b. Тогда,  будет соответствовать
будет соответствовать  , а
, а 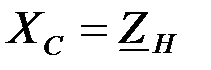 – в R-C ветви растущей из двух последовательно включенных сопротивлений
– в R-C ветви растущей из двух последовательно включенных сопротивлений  и
и  (рис.1.17).
(рис.1.17).
Рис.1.17 R-C ветвь исходной схемы
4) Выберем масштаб тока и напряжения: 
5) Отложим в масштабе (рис.1.18) векторы полного в напряжения  и тока в первой ветви
и тока в первой ветви  со сдвигом на угол
со сдвигом на угол  по отношению к общему напряжению (первая ветвь включает R-L элементы, следовательно
по отношению к общему напряжению (первая ветвь включает R-L элементы, следовательно  ).
).
6) Т.к. на основании первого закона Кирхгофа общий ток на входе контура:  , то конец вектора
, то конец вектора  принимаем за начало вектора тока
принимаем за начало вектора тока 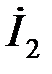 , а, следовательно, за начало построения круговой векторной диаграммы тока
, а, следовательно, за начало построения круговой векторной диаграммы тока  .
.
7) Вычисляем ток 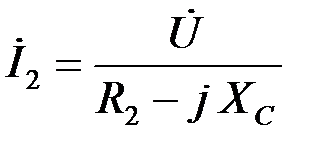 при коротком замыкании (шунтировании) изменяющегося сопротивления
при коротком замыкании (шунтировании) изменяющегося сопротивления  :
: 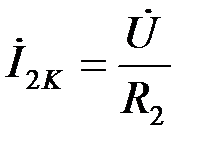 , откуда следует, что ток
, откуда следует, что ток  совпадает по фазе с напряжением
совпадает по фазе с напряжением  , приложенным к обеим ветвям
, приложенным к обеим ветвям  . Тогда, отложив
. Тогда, отложив  из конца вектора тока
из конца вектора тока  параллельно
параллельно  , получим хорду
, получим хорду  круговой диаграммы.
круговой диаграммы.
8) Выберем масштаб сопротивления  и отложим на хорде
и отложим на хорде  отрезок
отрезок 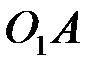 равный:
равный:  .
.
9) Из точки А под углом  к вектору тока короткого замыкания
к вектору тока короткого замыкания  (хорде
(хорде 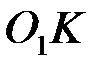 ) проводим линию переменного параметра AN:
) проводим линию переменного параметра AN:  .
.
В нашем случае  , где
, где
 ,следовательно
,следовательно  .
.
10) Восстанавливаем перпендикуляр в середине хорды  . Из точки
. Из точки  опускаем перпендикуляр на линию переменного параметра AN точка пересечения двух перпендикуляров дает центр КВД.
опускаем перпендикуляр на линию переменного параметра AN точка пересечения двух перпендикуляров дает центр КВД.
11) В точке 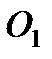 под углом
под углом  проводим касательную и восстанавливаем в этой же точке к ней перпендикуляр, перпендикуляр касательной и перпендикуляр хорды пересекутся в точке С. Это значит, что хорда
проводим касательную и восстанавливаем в этой же точке к ней перпендикуляр, перпендикуляр касательной и перпендикуляр хорды пересекутся в точке С. Это значит, что хорда  является диаметром окружности.
является диаметром окружности.
12) На линии AN откладываем 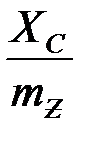 и соединяем точку
и соединяем точку 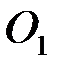 с концом отрезка
с концом отрезка  . При этом получаем
. При этом получаем 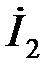 .
.
На диаграмме отмечены два резонансных режима, когда полный ток  – совпадает по фазе с полным напряжением
– совпадает по фазе с полным напряжением  при
при  '
'  .
.
Из круговой диаграммы следует также, что минимальное значение входного тока будет вблизи первого резонанса, но не при резонансе.
Если  , то в рассматриваемой цепи возможен только один резонанс (когда
, то в рассматриваемой цепи возможен только один резонанс (когда  совпадают по фазе)
совпадают по фазе)  – половина тока короткого замыкания (
– половина тока короткого замыкания ( ).
).

Рис.1.19 КВД для случая одного резонанса в параллельных ветвях
 Если
Если 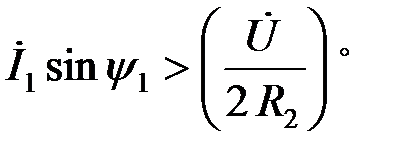 , то в рассматриваемой электрической цепи, ни при каких значениях параметров входной ток и напряжение по фазе не совпадают. Следовательно, резонансные явления в такой цепи невозможны.
, то в рассматриваемой электрической цепи, ни при каких значениях параметров входной ток и напряжение по фазе не совпадают. Следовательно, резонансные явления в такой цепи невозможны.
Если угол  , то КВД вырождается в линейную ВД, т.к. оказывается невозможно определить центр окружности и построить КВД.
, то КВД вырождается в линейную ВД, т.к. оказывается невозможно определить центр окружности и построить КВД.

Рис.1.20 КВД при отсутствии резонанса в параллельных ветвях
Дата добавления: 2015-10-21; просмотров: 159 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ПОРЯДОК ПОСТРОЕНИЯ КРУГОВОЙ ВЕКТОРНОЙ ДИАГРАММЫ (КВД) ТОКОВ | | | ПОРЯДОК ПОСТРОЕНИЯ КРУГОВЫХ ДИАГРАММ НЕРАЗВЕТВЛЕННЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ |