Характеристическая постоянная или мера передачи ЧП

Мера передачи ЧП определяется как отношение напряжений и токов на входе и выходе ЧП. У симметричного ЧП (СЧП) отношение напряжений и токов одинаково:

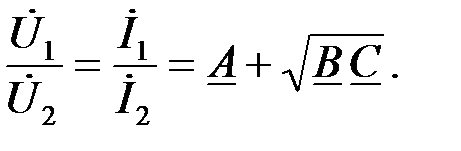(1.22)

Если отношение или вещественное число, то оно показывает, во сколько раз уменьшается напряжение или ток при передачи сигнала через ЧП.

Если отношение или 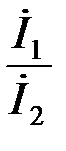комплексное число, то модуль комплексного числа определяет ослабление (усиление) передаваемого сигнала, а аргумент характеризует изменение фазы сигнала.

В электротехнике и радиотехнике изменение сигналов по амплитуде выражают в показательной форме и в логарифмических единицах:

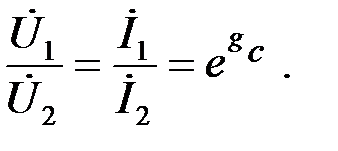(1.23)

Тогда, после логарифмирования, мера передачи СЧП имеет вид:

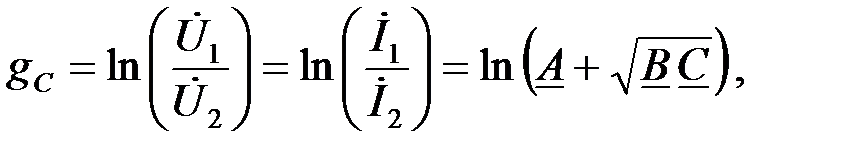(1.24)

где 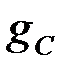– характеристическая постоянная или мера передачи ЧП.

В случае несимметрического ЧП «» определяют как отношение произведений комплексов входных напряжений и токов к произведению комплексов выходных напряжений и токов:

(1.25)

Если ЧП симметричен, то и уравнение (1.25) приводится к виду (1.24).

Выразим «» для СЧП через модули и фазы сигналов на входе и выходе ЧП:

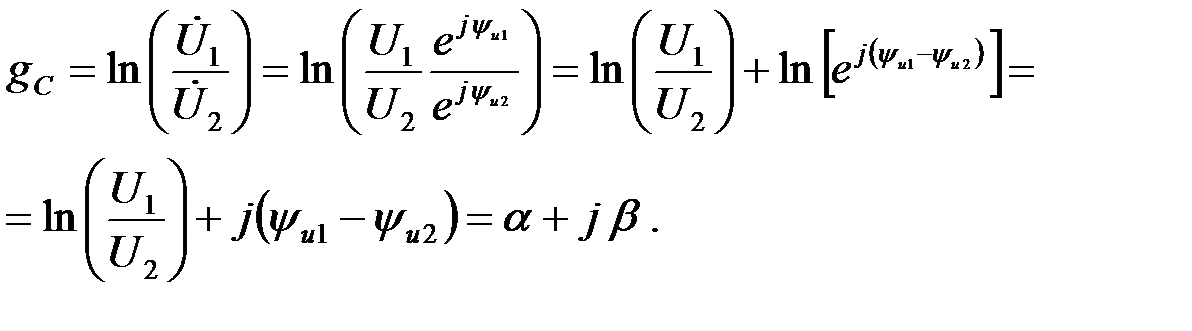(1.26)

Здесь показывает, как изменяется по модулю напряжение сигнала, передаваемого через ЧП. Поэтому «» называют коэффициентом затухания.

Величина показывает изменение фазы сигнала передаваемого через ЧП, поэтому «» называют коэффициентом фазы.

Единица измерения «» – радиан, а единица измерения «» – Белл (Б) или чаще дециБелл (дБ), иногда измеряют в неперах (Нп). При этом 1 Б = 10 дБ; 1 Б = 1,15 Нп. И наоборот 1 Нп = 8,686 дБ = 0,88686 Б.

Затухание в Белах определяют как:

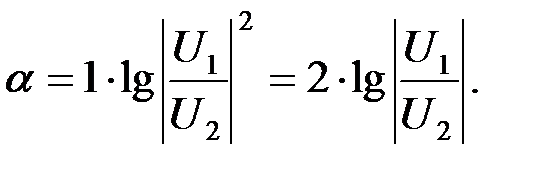(1.27)

Затухание в дБ определяют как:

(1.28)

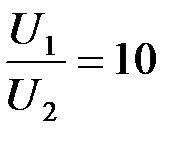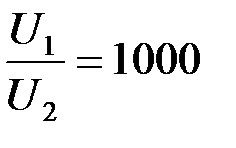Если , то если , то если , то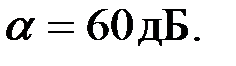

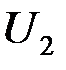Если задан коэффициент затухания, например, то потенцируя выражение (1.28), получим откуда следует, что ослабляется при примерно на 26 % по сравнению с .

В [1] показано, что обобщенные A, B, C, D коэффициенты ЧП можно выразить через характеристические параметры:

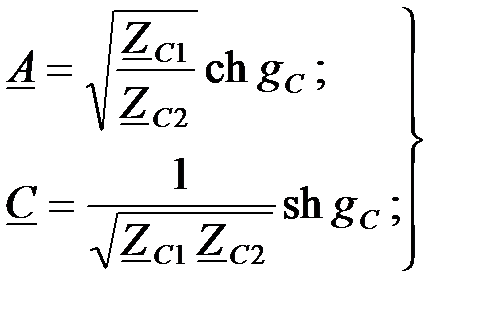
(1.29)

где гиперболический синус () и косинус (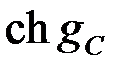) от постоянной передачи .

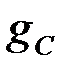(1.30)

так как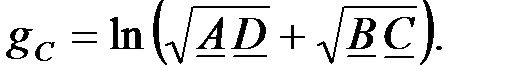

Подставляя A, B, C, D коэффициенты из (1.29) в уравнения ЧП в «А» – форме записи (1.1), получим уравнения ЧП, выраженные через характеристические параметры:

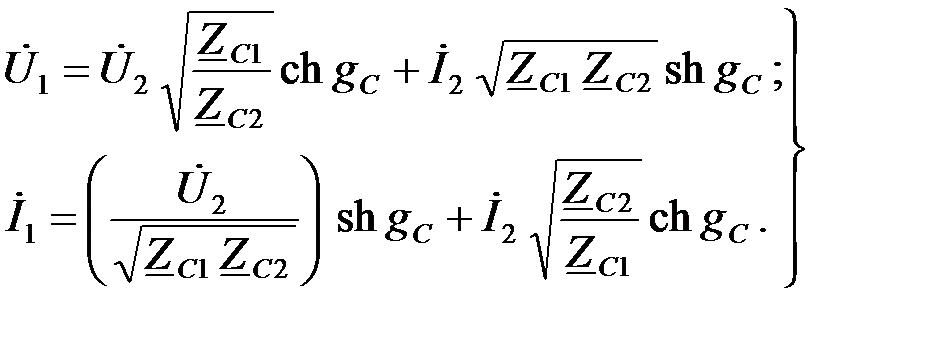(1.31)

Дата добавления: 2015-10-21