Построение дуги окружности по хоорде и вписанному углу

1) Вписанный угол – угол 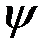, вершина которого находится на окружности, а стороны являются хордами.

2) Величина вписанного угла численно равна половине дуги, на которую он опирается.

Рис.1.9 Построение дуги окружности по хорде и вписанному углу  

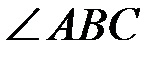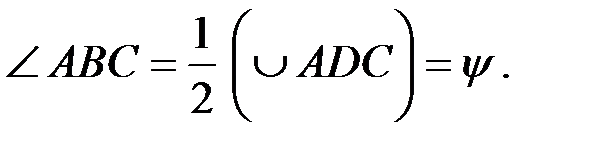– вписанный угол, , но с другой стороны Угол ADC опирается на дугу 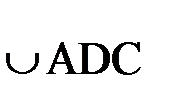, поэтому

Сумму двух вписанных углов ABC и ADC выразим через дуги:

Сумма двух вписанных углов ABC и ADC равна половине длины окружности, а в радианной мере равна «π» или 180° в градусной мере.

Угол CDE дополняет угол ADC до 180°, поэтому мы можем утверждать, что , но , т.к. сумма .

Замечательная особенность угла CDE состоит в том, что в какую бы точку не перемещалась вершина D угла ADC по дуге величина этого угла остается неизменной: . Для того чтобы вписанный угол ADC изменился по величине необходимо изменять величину дуги на который опирается угол ABC.

Угол между продолжением корды АС и касательной к окружности в данной точке С также равняется углу ψ или .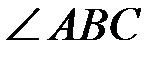

Дата добавления: 2015-10-21