Сезонные индексы

До сих пор мы предполагали, что данная модель временного ряда равна

или

.

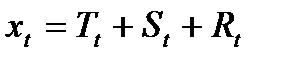Эти модели позволяют сезонной составляющей, , для одного и того же сезона быть разной в разные годы. Например, для квартальных данных, значение не должно быть таким же, как значения или , или 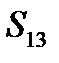. Однако часто правильно делать допущение о том, что сезонные составляющие являются одинаковыми от года к году, то есть, что эффект данного сезона является одинаковым в течение некоторого времени. Например, для квартальных данных 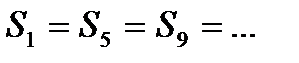, и так далее. В этом случае, значения оценок этих сезонных составляющих, 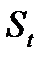, часто назывались сезонными индексами. Сезонные индексы измеряют эффект каждого сезона, и могут быть использованы для построения прогнозов временного ряда.

Мы можем получить сезонные индексы, используя оценку тренда временного ряда (вычисленные благодаря методу линейной регрессии или временному ряду центрированной скользящей средней), рассмотренного нами выше. Метод, который мы использовали, слегка отличается, в зависимости от того, допускаем мы или не допускаем, что для данного временного ряда подходит аддитивная или мультипликативная модель. Разница состоит в том, что мы делим для мультипликативной модели и вычитаем те же количества для аддитивной модели.

1. Вычисление сезонных индексов, если подразумевается использование мультипликативной модели.

Мы делаем допущение о том, что эта модель имеет вид:

.

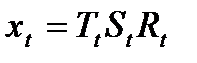Оценка тренда временного ряда, которую мы только что получили, является оценкой значения для каждого периода времени, поэтому, если мы разделим исходные данные, , на соответствующие значения оценки тренда временного ряда, мы получим значение .

Следующая таблица показывает эти вычисления для данных об изготовлении кухонь с использованием центрированной скользящей средней в качестве значения оценки тренда временного ряда. Проверьте, что Вы поняли, откуда берутся все элементы этой таблицы.

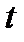
		Оценка тренда временного ряда (Центрированная СС)	Оценка тренда временного ряда
		*	*
		*	*
		20,625	0,8242
		21,125	0,9941
		21,625	1,1561
		21,875	1,0561
		22,25	0,8090
		22,5	0,9778
			1,1739
		23,5	0,9787
		23,75	0,9263
		24,5	0,8980
		25,25	1,1485
			1,0385
		26,75	0,8972
		27,25	0,9541
		27,375	1,1324
		27,5	1,0545
		27,75	0,8228
		27,75	1,0090
		27,875	1,1121
		28,25	1,0265
		28,75	0,8348
		*	*
		*	*

Мы оцениваем индекс для сезона, беря средние значения статей в четвёртом столбце, которые есть в этом сезоне. Легче всего это сделать, снова выписав содержание четвёртого столбца, со строкой для каждого сезона и со столбцом для каждого года, как показано ниже.

Сезон
1	2	3	4
		0,8242	0,9941
1,1561	1,0514	0,8090	0,9778
1,1739	0,9787	0,9263	0,8980
1,1485	1,0385	0,8972	0,9541
1,1324	1,0545	0,8288	1,0090
1,1121	1,0265	0,8348
Мультипликативный сезонный индекс
1,1446	1,0299	0,8534	0,9666

Поэтому, индекс сезона 1 равен 1,1446, индекс сезона 2 равен 1,0299 и так далее. Это означает, что значение данных, которые были собраны в первом сезоне, примерно на 15% выше, чем они были бы, если бы отсутствовал сезонный эффект, и для второго сезона это значение на 3% выше, чем оно могло быть, если бы не было сезонного эффекта.

Некоторые тексты будут содержать предложение усовершенствовать эти мультипликативные сезонные индексы и дальше, шкалируя их таким образом, чтобы они имели среднее значение, равное 1. Например, здесь сумма четырёх сезонных индексов равна 3,9945. Мы хотели бы, чтобы их сумма была равна 4, поэтому, если мы умножим каждый индекс на 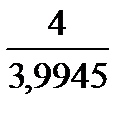, мы этого достигнем. Выверенные таким образом индексы превращаются в следующие индексы:

Сезон
Индекс	1,1462	1,0313	0,8546	0,9679

Дата добавления: 2015-10-13