Проверьте. Проходит месяц, и теперь это конец третьего месяца

Проходит месяц, и теперь это конец третьего месяца. Действительный спрос в третий месяц оказывается равным 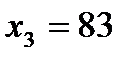. Вычислите экспоненциальный прогноз спроса в 4 месяц.

Решение:

.

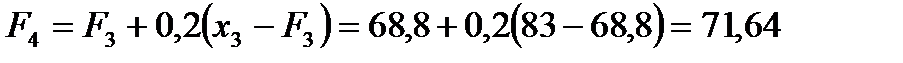Мы можем продолжать так делать прогнозы месяц за месяцем. Таблица 9.1 содержит действительные значения и прогнозы спроса на еду для кошек за последние 15 месяцев. Для простоты и ясности изложения, мы округлили каждый прогноз до 2 степеней свободы, прежде чем использовать их для дальнейших вычислений, хотя, на практике, мы, как правило, округляем до большего количество знаков после запятой. Значения, которые мы только что использовали и вычислили, выделены жирным шрифтом. Последний столбец показывает ошибку в каждом прогнозе.

Месяц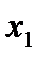
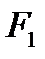
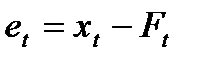
		67,00	9,00
		68,80	14,20
		71,64	6,36
		72,91	-4,91
		71,93	-12,93
		69,34	-0,34
		69,27	0,73
		69,42	-11,42
		67,14	1,86
		67,51	7,49
		69,01	-0,01
		69,01	2,99
		69,61	11,39
		71,89	-0,89
		71,71

Заметьте, что мы начали наши вычисления, используя значение 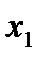в качестве прогноза для значения 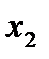, то есть, установив, что .

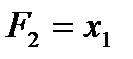Преимущество экспоненциального прогнозирования заключается в том, что вычисления очень просты, и поэтому, при необходимости, могут быть использованы для прогнозирования спроса для многих сотен различных продуктов, при этом не возникает необходимости в сложном программном обеспечении.

Различные значения α

До сих пор мы произвольно использовали 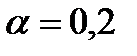, чтобы вычислить экспоненциальный прогноз. 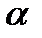называется сглаживающая постоянная, и она может принимать любое значение между 0 и 1. Давайте посмотрим на то, как выбор 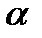действует на прогнозы.

Вспомним, что экспоненциальные прогнозы вычисляются с помощью формулы:

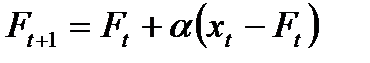, и что 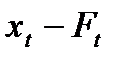есть самая последняя ошибка.

Если значение 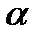близко к 0, только малая пропорция ошибки самого последнего прогноза будет включена в 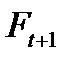, и поэтому новый прогноз не будет сильно отличаться от предыдущего. И наоборот, если значение 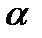близко к 1, большая пропорция ошибки последнего прогноза включена в 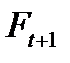, и поэтому на значение 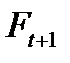сильно влияет последнее из наблюдавшихся значений, 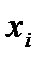. В крайних случаях, если 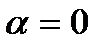, , 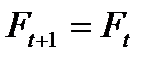и данные прогнозы абсолютно нечувствительны к новым данным, а если 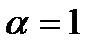, , поэтому самое последнее наблюдение используется в качестве прогноза, без учёта более ранних данных в этом временном ряду.

Это означает, что уместнее использовать малое значение 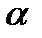(близкое к 0), если первоначальный временной ряд беспорядочный и неровный, поскольку каждое новое наблюдение не очень полезно при прогнозировании в будущем. И наоборот, большие значения 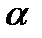(близкие к 1) уместны, если данный временной ряд достаточно ровный, и самая полезная информация получается из текущих наблюдений.

Рис. 9.7

В качестве иллюстрации, график на Рис. 9.7 показывает i) данные о еде для кошек за последние 15 месяцев, ii) значения прогнозов, которые были получены для каждого из месяцев с использованием 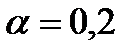(как было вычислено ранее) и iii) значения прогнозов для каждого месяца, полученные тем же путём, но с использованием 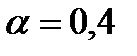. Это потому, что на временной ряд 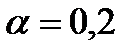в меньшей степени влияет каждое новое наблюдение. Заметьте также, что оба временных ряда прогнозов более ровные и менее рваные, чем первоначальные серии. По этой причине, этот метод часто называют экспоненциальным сглаживанием.

Другой способ выбрать подходящее значение 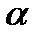― исследовать, насколько хорошо различные значения 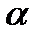предсказывали бы временные ряды в прошлом, но прежде, чем мы сможем это сделать, нам необходим способ оценки того, насколько «хороши» наши прогнозы.

Дата добавления: 2015-10-13