Выявление тренда с использованием регрессии

Другой способ выделить тренд временного ряда, в особенности, если данный тренд похож на линейный, сделать пригонку прямой к временному ряду, используя регрессию. То есть, мы используем временной ряд в качестве случайной величины Y, и время в качестве случайной величины Х, и используем модель линейной регрессии, как описано в Главе С8.

Следующая прямая была пригнана с помощью метода наименьших квадратов (?) к данным о кухням:

.

Рис. 9.11

Заметьте, что сезонный эффект приводит к тому, что временной ряд колеблется, намного отклоняясь от прямой. Как следствие, значение суммы квадратов ошибки может быть высоким, что делает коэффициент смешанной корреляции, 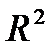, неестественно низким, так что это преуменьшает силу (?) прямой модели линейной регрессии (?). Для этих данных, .

Значение оценки тренда временного ряда, поэтому, включает в себя значения высот (?) прямой, то есть,

,

Соответствующее времени 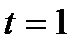, , 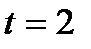… . Заметьте, что, в противоположность процедуре центрированной скользящей средней, мы не «теряем» никаких данных с обоих концов временного ряда.

Дата добавления: 2015-10-13