Некоторые модели временного ряда

Мы уже обозначили временной ряд , и мы сказали, что он может иметь сезонный эффект, эффект тренда (тенденцию?) или оба эти эффекта. Один из способов, с помощью которого эту мысль можно формализовать, сказать, что временной ряд есть сумма трендовой составляющей (которая может быть равной нулю) и сезонной составляющей (которая может быть равной нулю), и случайной составляющей, которая не имеет трендового или сезонного характера. То есть, мы говорим, что временной ряд образован аддитивной моделью,

,

Где есть трендовая составляющая, ― сезонная составляющая и ― случайная составляющая. Если использовать данную модель, сезонный эффект во время заключается в том, чтобы прибавить к уровню данного временного ряда (?). Это значит, что значение временного ряда повышается или понижается на то значение, которое зависит от сезона.

Альтернативной моделью, которая может подойти, является следующая модель:

.

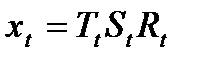Теперь перечисленные выше составляющие умножены друг на друга, поэтому мы называем данную модель мультипликативной моделью.

Согласно данной модели, эффект определённого сезона следует умножать на уровень (?) временного ряда на . То есть, значение данного временного ряда повышается или понижается на пропорцию, которая зависит от сезона. Мультипликативная модель, поэтому, подходит в тех случаях, когда, по мере того, как увеличивается или уменьшается тренд, сезонный эффект увеличивается или уменьшается. Такую модель часто используют для данных о продажах, потому что, если наблюдается устойчивый рост объёмов продаж в течение некоторого отрезка времени, различия между сезонами, как правило, тоже увеличиваются.

На графике временного ряда на Рис. 9.8 показаны два временных ряда с одинаковым трендом, но (а) имеет аддитивную сезонную составляющую, а (b) имеет мультипликативную сезонную составляющую. Заметьте, что кривая сезонного графика для аддитивной модели ровно восходит вместе с трендом, но для мультипликативной модели она становится более неровной вместе с трендом.

Разбивая наблюдаемые нами временные ряды 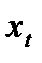на его составляющие, 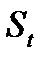, 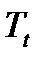и , мы можем выверить данные в соответствии с сезонным эффектом, и делать прогнозы на будущее.

Дата добавления: 2015-10-13