Проверьте. Вычислите сезонные индексы для временного ряда магазина тарелок спутникового

Вычислите сезонные индексы для временного ряда магазина тарелок спутникового телевидения, допуская, что мультипликативная модель подходит для данного временного ряда.

День
Центр. С.С.5,75 5,875 6,25 6,75 7,125 7,375 7,75 8,375
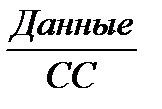1,2174 1,3617 0,48 0,8889 1,2632 1,3559 0,5161 0,8358

Сезон
1	2	3	4
		1,2174	1,3617
0,4800	0,8889	1,2632	1,3559
0,5161	0,8358
Мультипликативный сезонный индекс
0,4981	0,8624	1,2403	1,3588

Сумма индексов равна 3,9596, поэтому мы можем подогнать данные индексы, чтобы их сумма была равна 4, умножая на 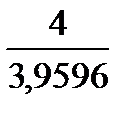, получим следующие значения: 0,5032, 0,8712, 1,2530 и 1,3727.

2. Вычисление сезонных индексов для аддитивной модели.

Если аддитивная модель является пригодной, мы действуем в точности тем же способом, только теперь мы вычитаем, когда раньше делили.

Мы иллюстрируем это, снова используя данные об изготовлении кухонь. Либо временной ряд центрированной скользящей средней, либо временной ряд, полученный с использованием методов регрессии, можно взять в качестве оценки тренда временного ряда.

Данная модель является аддитивной, что подразумевает, что

.

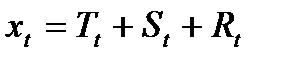Если мы вычтем оценку тренда временного ряда (оценку 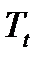) из исходных данных, мы получим оценки 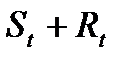, как показано в столбце (4) ниже.

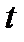
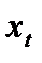
		Оцененный трендовый временной ряд (из регрессии)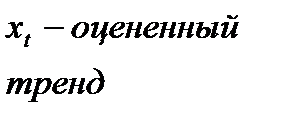
(1)	(2)	(3)	(4)
		20,1169	3,8831
		20,5338	-0,5338
		20,9508	-3,9508
		21,3677	-0,3667
		21,7846	3,2154
		22,2015	0,7985
		22,6185	-4,6185
		23,0354	-1,0354
		23,4523	3,5477
		23,8692	-0,8692
		24,2862	-2,2862
		24,7031	-2,7031
		25,1200	3,8800
		25,5369	1,4631
		25,9538	-1,9538
		26,3708	-0,3708
		26,7877	4,2123
		27,2046	1,7954
		27,6215	-4,6215
		28,0385	-0,0385
		28,4554	2,5446
		28,8723	0,1277
		29,2892	-5,2892
		29,7062	0,2938
		30,1231	2,8769

Поэтому временной ряд в столбце (4) состоит из значений оценок 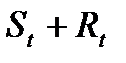. Значение оценки аддитивного сезонного индекса можно найти, определив среднее значение их для каждого сезона, как показано ниже. Подобным образом, эффект случайного фактора 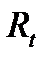сглаживается.

Сезон
1	2	3	4
3,8831	-0,5338	-3,9508	-0,367
3,2154	0,7985	-4,6185	-1,0354
3,5477	-0,8692	-2,2862	-2,7031
3,8800	1,4631	-1,9538	-0,3708
4,2123	1,7954	-4,6215	-0,0385
2,5446	0,1277	-5,2892	0,2938
2,8769
Аддитивный сезонный индекс
3,4514	0,4636	-3,7867	-0,7036

Результатом является набор аддитивных сезонных индексов ― по одному на каждый сезон.

В некоторых текстах эти значения выверены таким образом, что в сумме они дают 0. Чтобы этого достичь, они суммируют сезонные индексы, что даёт в сумме -0,5753 здесь и делится на 4, получается -0,1438. Прибавляем 0,1438 к каждому сезонному индексу, мы получим набор выверенных аддитивных сезонных индексов, сумма которых равна 0. Для этого примера, эти индексы таковы:

Сезон
Индекс	3,5952	0,6074	-3,6429	-0,5598

Дата добавления: 2015-10-13