ПП процесс в RLC цепи.

В соответствии с формулой (6) ток в RLC цепи будет состоять из трёх слагаемых для того, чтобы их определить нужно значение p₁ и p₁ , т.е. решить уравнение (4).

Корни уравнения (4) имеют вид 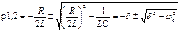(15)

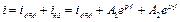(6)

;

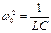
Рассмотрим поведение цепи, если к ней приложена постоянная ЭДС e(t)=E; U_C(0)=U’; i(0)=0.

Анализ поведения цепи в этих условиях показывает, что установившийся ток равен нулю (цепь содержит конденсатор, а полный ток (16) А₁=А₂

Рассмотрим процессы в цепи при различных соотношениях между δ и ω₀:

1) δ>ω_{0; ;}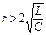

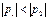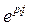; спадает медленнее, чем

апериодический

2) δ=ω₀; p₁=p₂=-δ

Исследуя этот режим можно показать, что график изменения тока аналогичен предыдущему - этот режим называется критическим.

3) δ>ω₀; p_1,2=-δ jω_св;

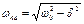
ω_св- частота свободных колебаний возникающие в RLC цепи при заданных начальных условиях, когда к ней приложено постоянное напряжение.

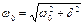
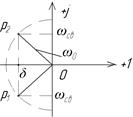
p₁=-δ+jω_св

p₂=-δ+jω_св

График тока протекающего в цепи в этом режиме будет представлять собой затухающие синусоидальные колебания, при этом режим цепи называется колебательным.

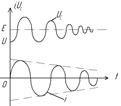
Таким образом в RLC цепи возможны условия возникновения синусоидальных колебаний при определённом подборе параметров этой цепи.

6.Операторный метод расчёта переходных процессов.

В технике часто пользуются изображениями чисел или функций, например: логарифм – это изображение числа комплексной величины, это изображение функции времени. В операторном методе каждой функции времени соответствует функция новый переменной p: p=a+jb

Переход от функции времени к функции р осуществляется с помощью прямого преобразования Лапласа. Функцию времени: f(t) называют оригиналом, ей соответствует функция F(р), которая называется изображением.

(*)

(**)

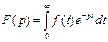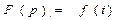Из курса математики известно, как выглядит изображение некоторых функций.

1)Изображение постоянной f(t)=A

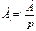
2) ;

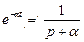
Если α=jω, то e^jωt соответственно 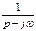; следовательно

3) Изображение первой производной

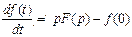
Отсюда следует, что напряжение на индуктивности 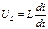можно преобразовать в виде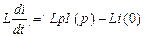

4) Изображение интеграла

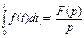
Таким образом напряжение на конденсаторе:

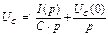
Операторный метод очень удобен для расчётов, поскольку дифференцирование заменяется умножением, а интегрирование делением.

Дата добавления: 2015-09-06