Разложение периодической несинусоидальной функции в тригонометрический ряд.

Такую функцию обычно представляют в виде ряда Фурье в общем случае он представляет собой сумму постоянной составляющей основной 1 гармоники с периодом равным периодом самой функции и высших гармоник у которых частоты в целое число раз больше частоты основной гармоники.

Для периодической не синусоидальной ЭДС можно записать:

(1)

E₀ – постоянная составляющая

- первая гармоника

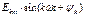- k-ая гармоника.

Сумма членов ряда стремится к , но на практике ограничиваются некоторым ограниченным числом ряда.

На практике часто удобно пользоваться рядом (1) записанным без начальных фаз, чтобы вычислить коэффициент этого ряда рассмотрим k-ую гармонику:

(2)

Тогда ряд примет вид:

(3)

Из курса математики известно, что:

; ;

; (4)

Таким методом находят нужные величины, если функция задана аналитически. Если функция задана графически используют ряд приближённых методов.

Расчёт цепей при не синусоидальных воздействия для линейных цепей по методу наложения, а именно раскладывают заданную функцию в ряд Фурье

Находит мгновенные токи возникают в цепи под действием каждого напряжения и суммируют их.

Так каждая составляющая есть либо постоянная составляющая либо синусоидальная функция времени, то для расчета каждой из них можно применить все методы расследования ранее.

Дата добавления: 2015-09-06