Законы Кирхгофа в операторной форме

I: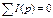

II:

Составляя изображения функции времени и представляя в виде двух полиномов.

Рассмотрим разветвленную схему и найдём в ней токи в операторном виде.

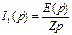
Найдём полное сопротивление цепи: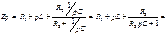

(2)

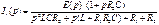(3)

Для нахождения тока I₃ запишем выражение для параллельных ветвей точек а и b:

(4)

Подставив сюда найденные значения I₁(p) найдём ток I₃(p)

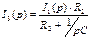(5)

Рассмотрим выражение (3) в зависимости от величины приложенной ЭДС:

1)Если приложена постоянная ЭДС, т.е. 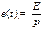в этом случае

I₁(p)= 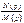степень полинома числителя меньше степени полинома знаменателя.

2) Если к цели приложено переменное напряжение.

e(t) =Em∙sin(ωt+ψ) --> комплексная форма: 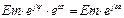, следовательно в операторной форме ЭДС будет представлено:

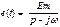
Если обозначить высшую степень оператора р в полиноме N(p) через n, а высшую степень оператора р в полиноме оператора М(р) m, то n<m. Во всех физически реализуемых цепях при воздействии любых встречающихся ЭДС всегда n<m.

Если решить уравнение М(р)=0, найдём соответственно m-корней. Часть из них определяется характером приложенных ЭДС; остальные корни обусловлены свойствами самой цепи её конфигурации.

Дата добавления: 2015-09-06