Построение профиля кулачка коромыслового кулачкового механизма

Главным этапом синтеза кулачкового механизма является построение профиля кулачка, в основу которого положен метод обращенного движения. Суть этого метода заключается в том, что всем звеньям механизма условно сообщается дополнительное вращение с угловой скоростью, равной угловой скорости кулачка, направленной в обратную сторону. Тогда кулачок остановится, а стойка вместе с толкателем (коромыслом) придет во вращательное движение вокруг центра кулачка О с угловой скоростью w_к. Кроме того, толкатель будет совершать ещё движение относительно стойки по закону, который определяется профилем кулачка.

Из центра О проводим окружности радиусами r_min и l_OА. Определяем положение центра ролика коромысла, для чего из точки А радиусом, равным длине коромысла, проводим дугу до пересечения с окружностью радиуса r_min. Точка пересечения В₀ и есть положение центра ролика коромысла, соответствующее началу удаления. На траекторию точки В коромысла наносим разметку ее согласно диаграмме S(φ). Получаем точки B₁, B₂, B₃,…, B₆.

От линии центров ОА в сторону, противоположную вращению кулачка, откладываем фазовые углы j_У и j_В, разделим на 6 равных частей. Полученные точки С₁, С₂, С₃ и т.д. дадут положения центра вращения коромысла в обращенном движении.

Находим положения центра ролика в обращенном механизме. Дли этого производим следующие построения: из центра вращения кулачка О радиусами, равними ОB₁, ОB₂, ОB₃ и т.д., проведем дуги окружностей, а из точек С₁, С₂, С₃ и т.д. длиной коромысла l_АВ сделаем засечки на соответствующих дугах (точки 1^', 2^', 3^', …, 13^'). Соединив полученные точки 1^', 2^', 3^', …, 13^' плавной кривой, получим центровой (теоретический) профиль кулачка, соответствующий углу удаления.

Аналогично строим центровой профиль кулачка, соответствующий углу возвращения. Разметку траектории точки В (центра ролика) при возвращении наносим на дугу радиуса l_АВ, проведенную из точки С₁₃ (точки B₇, B₈, B₉,…, B₁₃).

Для определения действительного профиля кулачка необходимо определить радиус ролика. Из конструктивных соображений радиус ролика не рекомендуется принимать больше половины минимального радиуса

r_p £ (0,4 ¸0,5) r_min

r_p = 0,35×0,0195 = 0,0068 м.

Принимаем r_p равным 7 мм.

Действительный (практический) профиль кулачка получим, если построим эквидистантную кривую радиусом, равным r_{p .}

5.2 Проектирование эвольвентного внешнего зацепления прямозубых цилиндрических колёс

Спроектировать эвольвентную зубчатую передачу внешнего зацепления, колёса которой нарезаны стандартной рейкой. Принимаем, что зубчатые колёса изготовлены без смещения исходного контура (х₁ = х₂ =0). Тогда угол зацепления равен углу профиля инструмента (a_w = a =20°), делительные окружности являются одновременно начальными окружностями зацепления (r_w1 = r₁ и r_w2 = r₂).

Рассчитываемая зубчатая передача имеет следующие параметры:

Z₁ =15; Z₂ =21; m =8.

Радиусы начальных окружностей колёс.

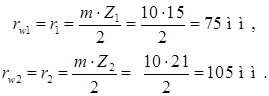
Радиусы основных окружностей колёс

Радиус окружностей вершин зубьев

где =1 - коэффициент высоты головки зуба,

- высота головки зуба (расстояние по радиусу между делительной окружностью и окружностью вершин).

Радиусы окружности впадин колёс.

где С^* =0,25 - коэффициент радиального зазора;

С^* m=С - радиальный зазор.

Шаг по делительной окружности

Р=p × m= 3,14×10=31,4 мм.

Окружная толщина зуба по делительной окружности

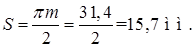
Межосевое расстояние

Для построения картины зацепления зубчатых колёс выбираем масштаб 4:1. Тогда высота зуба равная

будет отображаться на чертеже отрезком 72 мм.

Построение зубьев проводим в следующем порядке:

- Откладываем межосевое расстояние a_w (O₁O₂ на чертеже);

- Радиусами r_w1 и r_w2 проводим начальные окружности колес. Точка P касания их является полюсом зацепления;

- Проводим основные окружности колес, окружности вершин зубьев и окружности впадин;

- Через полюс зацепления P проводим общую касательную t-t к начальным окружностям колес и линию зацепления n-n, касающуюся в точках A и B основных окружностей. Часть ab линии n-n, заключенная между окружностями вершин зубьев, называется активной линией зацепления, т.е. геометрическим местом действительного касания профилей зубьев;

- Строим эвольвенты профилей зубьев, соприкасающихся в полюсе зацепления P. Профили зубьев получают обкатывая линию зацепления как по одной, так и по другой основным окружностям. При обкатывании точка P линии зацепления описывает эвольвенты e₁e₁ и e₂e₂, которые являются искомыми профилями. Для построения эвольвентного профиля зуба первого колеса отрезок AP делим на равные части (в нашем случае на 4). На основной окружности первого колеса вправо и влево от точки A откладываем дуги, длины которых равны этим отрезкам, получаем точки 1',2',3',4',5',6' и 7'. Через эти точки проводим касательные к основной окружности радиуса rb (перпендикуляры к соответствующим радиусам). На касательной, проведенной через эту точку 1', отложим 1/4 отрезка AP. На касательной, проведенной через точку 2 отложим 2/4 отрезка AP и т.д. Проведя аналогичные построения на каждой из касательных, получим ряд точек 1'', 2'', 3'',...,7''. Плавная кривая, проведенная через полученные точки, является эвольвентным профилем правой части зуба первого колеса. Таким же способом строится эвольвентный профиль зуба второго колеса (для этого используется отрезок BP);

Профиль ножки зуба, лежащий внутри основной окружности, очерчивается по радиальной прямой, соединяющей начало эвольвенты с началом колеса, и сопрягается с окружностью впадин закруглением радиуса P =0,4 m. По начальной окружности откладываем половину толщины зуба , проводим ось симметрии зуба (радиальную прямую) и по законам симметрии строим левый профиль зуба;

- На каждом колесе справа и слева от построенного по точкам зуба строим еще два зуба (с помощью шаблонов или лекал). При вращении первого колеса (допустим в направлении вращения часовой стрелки) ножка его зуба войдет в зацепление в точке a с головкой зуба второго колеса. В точке b головка зуба первого колеса выйдет из зацепления с ножкой зуба второго колеса. Таким образом, точка зацепления (соприкосновения зубьев) перемещается по профилю зуба первого колеса от его основания к вершине, а по профилю зуба второго - наоборот, от вершины к основанию.

Участки профилей зубьев, которые в процессе передачи вращения входят в соприкосновение друг с другом, называют активными профилями. Определим эти участки. Точку f₁ на профиле зуба первого колеса получим, если из центра O₁ описать дугу af₁ радиусом O₁a. Точно также находим точку f_a, описав дугу af₂ радиусом O₂b.

В точке a встретятся точки f₁ и e₂, а в точке b выйдут из зацепления точки e₁ и f₂. Активными профилями являются части эвольвент e₁f₁ и e₂f₂.

Чтобы построить дугу зацепления на первом зубчатом колесе, профиль этого колеса повернем вокруг точки O₁ и совместим последовательно с началом и концом активной линии зацепления, т.е. с точками a и b. На начальной окружности первого колеса получим дугу c'd'. Если повернем профиль зуба второго колеса вокруг точки O₂ и совместим с точками a и b, то на начальной окружности второго колеса получим дугу c''d''. Дуги c'd ' и c''d'' являются дугами зацепления по начальным окружностям, дуги ab' и a'b дугами зацепления по основным окружностям.

Длина дуги зацепления по основной окружности колеса равна длине g_a активной линии зацепления ab.

Углы j_a1 и j_a2 называются углами перекрытия. Отношение угла перекрытия зубчатого колеса к его угловому шагу называется коэффициентом перекрытия.

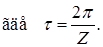
Вычислим коэффициент перекрытия проектируемой передачи. Из чертежа длина активной линии зацепления g_a = ab =180,4 мм.

Коэффициент перекрытия также можно определить по формуле:

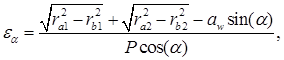
Коэффициент перекрытия называется среднее число зубьев, одновременно находящихся в зацеплении. Если ε_α = 1,52 то 52% времени в зацеплении находятся 2 пары зубьев, а остальное время - одна пара.

Удельное скольжения профилей зубьев (n₁ и n₂) является характеристикой скольжения одного профиля одного зуба по второму, то есть характеризует износ профилей, вызванный появлением сил трения.

Удельное скольжение можно определить по формулам:

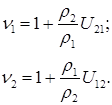
где ρ₁ - радиус кривизны эвольвенты первого зуба в точке зацепления;

ρ₂ - радиус кривизны эвольвенты второго зуба в точке зацепления;

U₁₂ и U₂₁ – передаточное отношение.

Вычислим удельное скольжение в нескольких точках зацепления и построим диаграммы удельного скольжения.

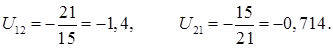
Результаты вычисления n₁ и n₂ занесём в таблицу 5.1.

Таблица 5.1 - Расчёт удельного скольжения.

x=r1
ga-x=r2
n1	-∞	-5,43	-1,86	-0,67	-0,07	0,29	0,52	0,69	0,82	0,92	1,00
n2	1,00	0,84	0,65	0,40	0,07	-0,40	-1,10	-2,27	-4,60	-11,60	-∞

Толщину зуба первого колеса по окружности вершин определим по формуле:

где a_a - угол профиля эвольвенты на окружности вершин зубьев;

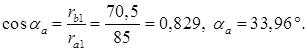
inv 20°=0,014904; inv 33,96°=0,081097.

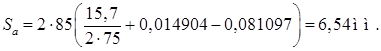
Для нормальной работы зубчатой передачи необходимо, чтобы соблюдались следующие условия:

1) e_a ³1,1;

2) S_a ³0,3 m (отсутствие заострения головки зуба у меньшего колеса).

В нашем случае оба условия удовлетворяются.

Таким образом, при решении вопроса относительно выбора и изготовления зубчатой передачи в каждом отдельном случае необходимо исходить из анализа эксплуатационных свойств передачи - продолжительности зацепления и удельного скольжения эвольвентных профилей зубьев.

Кинематическое исследование планетарного зубчатого механизма

Передаточное отношение зубчатой передачи

Передаточному отношению присваивается знак минус при внешнем зацеплении, знак плюс - при внутреннем. Знак передаточного отношения указывает направление вращения ведомого звена по отношению к ведущему.

Планетарным называется механизм, в котором геометрические оси некоторых зубчатых колёс являются подвижными. Простой планетарный механизм обладает одной степенью свободы(W =1).

В предлагаемых заданиях сложный планетарный механизм состоит из 2-х ступеней двухрядного планетарного механизма и пары колёс с неподвижными осями.

Наиболее точным из них является аналитический метод, известный как метод Виллиса, в основе которого лежит принцип обращения движения звеньев. Сущность этого метода состоит в том, что сообщается дополнительное вращение всем звеньям механизма вокруг их геометрических осей со скоростью - T_н , в результате чего водило H, вращаемое со скоростью + T_н, в обращённом движении будет неподвижно и механизм будет иметь все оси вращения зубчатых колес неподвижные. Передаточное отношение такой передачи можно определить по зависимостям, полученным для сложных зубчатых передач с неподвижными геометрическими осями. Менее точным, но весьма наглядным и простым, является графический метод Л.М.Смирнова.

Аналитическое исследование планетарного механизма

На рисунке дана схема сложного планетарного зубчатого механизма, у которого ступени1-2 и 5`-6 являются передачами с неподвижными осями и ступень 2`-Н представляет собой планетарный механизм. Передаточное отношение такого редуктора равно произведению передаточных отношений отдельных ступеней:

а передаточное отношение планетарной ступени определяется по формуле:

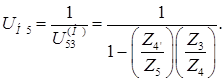
После этого уравнение примет следующий вид:

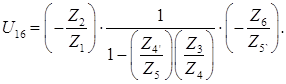
Поскольку известны числа зубьев колес 1 и 2, то можно определить передаточное отношение ступени 1-2.

Передаточное отношение ступени 5`-6 примем равным -1,1:

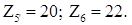
Из уравнения определим передаточное отношение от водила Н к колесу 5:

Из уравнения имеем:

Число зубьев определяется из условия соосности. Откуда вытекает равенство межосевых расстояний пар зубчатых колёс:

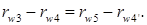
где r_w - радиусы начальных окружностей колёс.

При одном и том же модуле условие соосности можно представить равенством:

Из равенств подбираем числа зубьев колес 3, 4, 4’, 5:

Проверочный расчёт:

Передаточное отношение спроектированного механизма отличается от заданного на небольшую величину:

Графическое исследование планетарного механизма.

Для планетарных механизмов с цилиндрическими колёсами план линейных скоростей строится следующим образом.

Вычерчивается кинематическая схема механизма в масштабе длин, определяемых по формуле

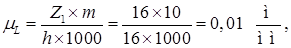
где h₁-длина отрезка в мм, изображающего на чертеже делительный диаметр зубчатого колеса.

Проводим прямую РР, параллельную линии центров колёс, и проектируем на неё оси колёс и все точки зацепления.

Скорость точки А изображается отрезком р₁a, перпендикулярным к прямой РР. Соединив точку а с точкой О₁, получим картину, изображающую распределение скоростей по звену 1. Линейная скорость точки О₂ равна нулю, поэтому, если провести луч аО₂ до пересечения с линией, проведённой через ось О₄, получим картину распределения скоростей по звену 2. Линия О₂ h будет являться картиной распределения скоростей водила.

У колеса 4 известны скорость точки, совпадающей со скоростью водила Н и скорость точки В (она равна 0). Поэтому, соединяя точки h и b, получим прямую, которая является картиной скоростей колеса 4.

Если продлим отрезок, проведенный через точки h и b, до пересечения с линией, проведенной через точку С, то получим картину распределения скоростей колеса 4’ hc.

Отрезок, проведенный через точку с до пересечения с линией, проведенной через ось О₅ будет являться картиной распределения скоростей колеса 5.

Соединив точку пересечения отрезка сО₅ и линии, проведенной через точку D, с точкой вращения колеса, получим распределение скоростей для шестого колеса.

Затем строим картину угловых скоростей. Проведём перпендикулярно к РР прямую ММ и обозначим на ней точку О. На произвольном расстоянии b от этой точки по вертикали отметим точку S. Считая эту точку полюсом, проведём от неё лучи, параллельные линиям распределения линейных скоростей звеньев механизма. Так как угловые скорости звеньев графически пропорциональны тангенсам углов, образуемых линиями распределения скоростей с прямой yy, то точки пересечения этих прямых с прямой ММ отсекают на ней отрезки, пропорциональные угловым скоростям соответствующих звеньев.

Измерив на картине угловых скоростей отрезки 01' и 06', определим:

Погрешность расчета:

ЗАКЛЮЧЕНИЕ

По первому листу курсового проекта был проведён структурный и кинематический анализ механизма двигателя путём построения планов скоростей и ускорений для положений механизма.

На втором листе выполнено кинематическое исследование плоского рычажного механизма, путём разбиения на звенья и строя план сил для каждого звена. А так же определение уравновешивающей силы по методу Н.Е. Жуковского.

Маховик применяется для увеличения приведённых масс или приведённых моментов инерции. Задачей маховика вялятся уменьшение амплитуды периодических колебаний скорости начального звена, обусловленных свойствами самих механизмов машин или периодическим изменением соотношения движущих сил и сил сопротивления. Маховик является аккумулятором кинетической энергии механизма (накапливая энергию во время ускорения и отдавая её при замедлении). Произведение массы обода на квадрат его диаметра носит название махового момента или характеристики маховика. Чем больше угловая скорость звена, тем меньше должен быть момент инерции маховика, а значит и его размеры. Поэтому выгодно, с точки зрения уменьшения массы маховика, а следовательно и затрат на его изготовление, устанавливать его на звеньях, обладающих большими угловыми скоростями.

По третьему листу курсового проекта было выполнено построение профиля кулачка по заданным законам движения в фазах угла удаления и возвращения, максимальному ходу толкателя, спроектирована пара цилиндрических прямозубых колёс в их эвольвентном зацеплении и построена диаграмма скольжения для этого зацепления.

В курсовом проекте также выполнено исследование планетарного зубчатого механизма аналитическим и графическим методами.

Дата добавления: 2015-10-13