Построение диаграмм движения коромысла

Строим диаграмму аналога ускорения толкателя , для чего на оси абсцисс откладываем в произвольном масштабе m_j заданные углы j_У =125°, j_ДС =45°, j_В =110°. Для принятой длины диаграммы Х =280 мм, величины отрезков, изображающие фазовые углы, будут:

где

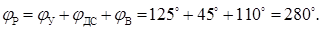
Для построения графика перемещения выходного звена по углу поворота кулачка необходимо выполнить двукратное интегрирование второй производной от перемещения выходного звена по углу поворота кулачка.

В интервале угла удаления j_У в произвольном масштабе строим параболический закон изменения ускорения, а в интервале угла возвращения j_В – по косинусу. Для построения аналога скорости интегрируем построенную диаграмму , для чего отрезки Х_У и Х_В делим на 6 равных частей.

Через точки 1, 2, 3…13 проводим ординаты, которые делят всю площадь заданных диаграмм на ряд участков. Площадь каждого из участков заменяем равновеликим прямоугольником с общим основанием на оси абсцисс. Проецируем высоты полученных треугольников на оси ординат. Точки 1 ‘, 2 ‘, 3 ‘^ê… 13 ‘ соединяем с полюсом Р₂ , взятым на произвольном расстоянии Н₂ от начала О осей координат лучами Р₂ 1 ‘, Р₂ 2 ‘, Р₂3 ‘… Р₂13 ‘^ê.

Ось абсцисс диаграммы , делим на такое же количество равных частей, как и ось абсцисс диаграммы . Из точки О параллельно лучу Р₂1проводим линию до пересечения её в точке 1 ‘‘ с ординатой 1. Повторяя данные построения, получим точки приближенной интегральной кривой. Соединённые точки образуют функцию .

Диаграмму перемещения толкателя S(j) также строим методом графического интегрирования кривой .

Вычислим масштабы диаграмм:

Масштаб по оси ординат диаграммы перемещений:

где h - максимальный ход толкателя;

S - максимальная ордината диаграммы перемещений.

В интервале угла удаления:

В интервале угла возвращения:

Масштаб по оси ординат диаграммы :

Масштаб по оси ординат диаграммы :

Разметку траектории точки В (центра ролика) производят в соответствии с диаграммой S(j), для чего слева от оси ординат под произвольным углом проводят прямую и на ней откладывают отрезок ОВ₆ в масштабе m_{L ,} равный максимальному перемещению толкателя. Конечную точку 6 соединим с точкой 6’ проекции наибольшей ординаты 6 – 6. Через точки 1‘, 2‘, 3‘, … 5‘ проводим прямые параллельные 6‘ – В₆. Полученные точки В₁, В₂, В₃, … В₆ дают разметку траектории толкателя в интервале удаления.

Аналогично осуществляем разметку траектории точки В для угла возвращения.

Определение минимального радиуса кулачка r_min и межосевого расстояния в коромысловом кулачковом механизме.

Из произвольной точки А проводим дугу радиусом равным длине коромысла l, отмечаем точку В₀ – начальное положение центра ролика коромысла.

От точки В₀ откладываем ход центра ролика В₀В₆ = h и переносим на него разметку траектории при удалении и возвращении.

По диаграмме определяем максимальные значения при удалении и возвращении коромысла:

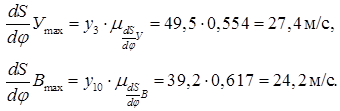
Из точки В₃ по лучу АВ₃ откладываем отрезок в направлении вращения кулачка, а в противоположную сторону отрезок . Аналогично определяем другие отрезки для остальных положений и строим диаграмму , к которой проводим касательные под углом g_min =55°. Точка пересечения этих касательных определит положение центра вращения кулачка - точку О (а заштрихованная площадь является областью возможного расположения кулачка).

Минимальный радиус кулачка равен:

r_min= OB₀ × m_S = 39×0,0005 = 0,0195 м,

Расстояние между центрами вращения кулачка и коромысла:

l_OА = OА × m_l =174,4×0,0005=0,0872 м.

Дата добавления: 2015-10-13