Кинематическое исследование механизма

Построение плана положений механизма компрессора

План положений механизма является основой для построения кинематических диаграмм линейного перемещения ползуна, или углового перемещения звена. Построение плана положений механизма выполняется в масштабе m_l. Схема механизма выполнена в масштабе М 1:2, следовательно, m_l = 0,002 м/мм. В этом масштабном коэффициенте вычерчивается кинематическая схема механизма. На траектории точки B ползуна 3 находим её крайнее положение. Для этого из точки О радиусом OB₀ = OА + АB делаем одну засечку на линии x-x и определяем верхнее крайнее положение, а радиусом OB₆ = АB - OА другую засечку – нижнее крайнее положение. Точки B₀ и B₆ будут крайними положениями ползуна 3. За нулевое положение принимается верхнее крайнее положение, а вращение кривошипа – по часовой стрелке. Начиная с нулевого положения кривошипа детали делим траекторию точки А на 12 равных частей и методом засечек находим остальные положения звеньев механизма. Для каждого положения находим точки S₂ и S₄, соединив последовательно все положения точки S, мы получим шатунные кривые.

Построение планов скоростей

Определение скоростей точек звеньев механизма, указанных на кинематической схеме, производим методом планов в последовательности, определённой строением механизма. Вначале определим линейную скорость точки А.

где w₁ - угловая скорость звена ОА, рад/с;

l_OA - длина звена ОА, м;

n₁ - частота вращения звена ОА, об/мин.

Подставим значения из задания:

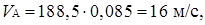
Скорости точки А будет одинакова для всех положений механизма. Масштабный коэффициент плана скоростей выбираем стандартным. Вектор pa, изображающий скорость точки А, имеет длину не менее 50-70 мм.

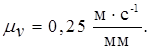
Построим вектор pa, это перпендикуляр кривошипу ОА, направленный в сторону его вращения.

Определим скорость точки D, принадлежащей группе Ассура (2, 3). Рассмотрим движение точки D по отношению к точке А, а затем по отношению к точке D₀ (принадлежащей неподвижному звену). Запишем векторные уравнения, которые решаются графически:

Согласно первому уравнению, через точку а на плане скоростей проводим прямую перпендикулярную DА, а согласно второму – через точку p (т.к. V_Do = 0) проводим прямую параллельную направляющей x-x.

Пересечение этих прямых определяет положение точки d, изображающей конец векторов V_D и V_АD. Из плана скоростей имеем:

Скорость точки S₂ и определяем по теории подобия:

Откуда:

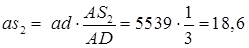мм.

Следовательно:

Скорости точек, точек принадлежащих группе Ассура (2, 3) определены.

Переходим к построению плана скоростей для группы (4, 5). Рассмотрим движение точки C относительно точки В, а затем по отношению к точке С₀, принадлежащей неподвижной направляющей. Запишем два векторных уравнения, которые решим графически:

Согласно первому уравнению через точку b плана скоростей проводим прямую перпендикулярную к ВС, а для решения второго уравнения необходимо через полюс р провести прямую параллельную направляющей y-y. На пересечении этих линий будет находиться точка с. Величины скоростей определим, умножая длины векторов на μ_v, получим:

Скорость центра масс S₄ звена 4 определим по теореме подобия.

Откуда:

мм.

Следовательно:

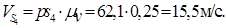
Определим угловые скорости звеньев из уравнений:

В указанной последовательности производятся построения планов для всех 12 положений механизма. Причём векторы, выходящие из полюса р, изображают абсолютные скорости точек, а отрезки соединяющие концы этих векторов – относительные скорости точек.

Вычисленные таким образом значения заносим в таблицу 2.1.

Таблица 2.1 - Данные графических построений планов скоростей

№	VА	VАB	VS2	VB	VАС	VS4	VС	ω1	ω2	ω4
м/с	рад/с
		14,0	12,6	9,9	8,2	14,3	12,0	188,5	43,27	25,46
		8,2	15,4	15,7		16,0	16,0	188,5	25,46
			16,0	16,0	8,2	15,4	15,7	188,5		25,46
		8,2	14,3	12,0	14,0	12,6	9,9	188,5	25,46	43,27
		14,0	11,8	6,2	16,0	10,7		188,5	43,27	49,54
		16,0	10,7		14,0	12,6	9,9	188,5	49,54	43,27
		14,0	11,8	6,2	8,2	15,4	15,7	188,5	43,27	25,46
		8,2	14,3	12,0		16,0	16,0	188,5	25,46
			16,0	16,0	8,2	14,3	12,0	188,5		25,46
		8,2	15,4	15,7	14,0	11,8	6,2	188,5	25,46	43,27
		14,0	12,6	9,9	16,0	10,4		188,5	43,27	49,54
		16,0	10,7		14,0	11,8	6,2	188,5	49,54	43,27

Направление угловой скорости звена АD определится, если вектор аd перенести относительно точки А параллельно самому себе в точку Dна схеме механизма и установить направление вращения звена АDотносительно точки А под действием этого вектора. Направление угловой скорости шатуна 4 определяет вектор аb, если его перенести из плана скоростей в точку С на схеме механизма.

Построение планов ускорений

Последовательность построения плана ускорений также определяется строением механизма. Вначале найдём ускорение ведущей точки А. При ω₁ = const начального звена, точка А имеет только нормальное ускорение:

Ускорение точки А изобразим на плане ускорений вектором πа, который направлен по звену ОА от точки А к точке О. Масштабный коэффициент выбираем стандартным и таким, чтобы длина вектора πа была в пределах 50 – 80 мм.

Вектор πа и есть план ускорений начального звена ОА. Теперь построим план ускорений группы (2, 3). Рассмотрим движение точки D относительно А и точки D относительно D₀.

Ускорение точки D определяется графическим решением следующих двух уравнений:

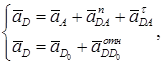
где а_DАⁿ - нормальное ускорение точки D по отношению к точке А;

а_DА^τ - тангенциальное ускорение точки D по отношению к точке А;

а_Do - ускорение точки D₀ направляющей x-x;

а_DDo^отн - ускорение точки D ползуна относительно точки D₀ направляющей.

В первом уравнении нормальное ускорение а_DАⁿ направлено по шатуну АD (от точки D к А). Величина ускорения:

Тангенциальное ускорение а_DА^τ перпендикулярно к звену и определяется из построения плана ускорений.

Ускорение а_Dо = 0, а относительное ускорение a_DDо^отн точки В ползуна относительно точки D₀ направляющей определяется построением плана ускорений.

В соответствии с первым уравнением на плане ускорений через точку а проводим прямую, параллельную звену АD, и откладываем на ней в направлении от точки D к точке А вектор аn₁, представляющий в масштабе μ_а ускорение а_DАⁿ _.

Через точку n₁ проводим прямую в направлении вектора тангенциального ускорения а_DА^τ перпендикулярно звену АD.

В соответствии со вторым уравнением через полюс π и совпадающую с ним точку D₀ проводим прямую в направлении ускорения а_DDo параллельно направляющей x-x. Точка пересечения этих прямых даст точку с, определяющую конец вектора абсолютного ускорения точки D.

Величина тангенциального ускорения:

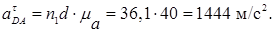
Ускорение центра масс S₂ звена АD определяется из пропорции:

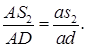
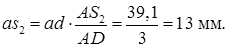
Тогда ускорение точки S₂ найдём по формуле:

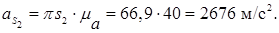
А сейчас определим ускорения точек звеньев 5 и 4. Запишем два векторных уравнения, рассматривая движение точки С относительно точки В и по отношению к точке С₀.

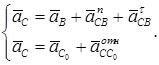
Вектор нормального ускорения а_СВⁿ направлен параллельно ВС от точки С к точке В. Величина этого ускорения:

На плане ускорений через точку с проводим прямую, параллельную звену ВС и откладываем наней в направлении от точки С к точке В вектор bn₂, представляющий в масштабе μ_а ускорение а_СBⁿ.

Через точку n₂ проводим прямую в направлении вектора тангенциального ускорения а_СВ^τ перпендикулярно звену ВС.

В соответствии со вторым уравнением через полюс π и совпадающую с ним точку С₀ проводим прямую в направлении ускорения а_ССo параллельно направляющей y-y. Точка пересечения этих прямых даст точку с, определяющую конец вектора абсолютного ускорения точки С.

Величина тангенциального ускорения:

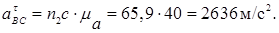
Ускорение центра масс S₄ звена ВС и определяется с помощью теоремы подобия.

Тогда ускорение точки S₄ найдём по формуле:

Определим величины угловых ускорений звеньев:

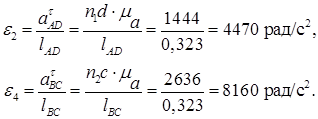
Направление углового ускорения ε₂ шатуна 2 определим, если перенесём вектор n₁d, из плана ускорений в точку D звена АD. Под действием этого вектора звено вращаться вокруг точки А по часовой стрелке. Направление углового ускорения ε₄ шатуна 4 определит вектор n₂c, перенесённый в точку C на схеме механизма. Это звено будет вращаться вокруг точки C против часовой стрелки.

В такой же последовательности производим построение плана ускорения для второго заданного положения механизма.

---

Дата добавления: 2015-10-13